【题目】若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如![]() ,
,![]() ).已知智慧数按从小到大的顺序构成如下数列:
).已知智慧数按从小到大的顺序构成如下数列:![]() 则第
则第![]() 个智慧数是__________.
个智慧数是__________.
参考答案:
【答案】2695
【解析】
如果一个数是智慧数,就能表示为两个正整数的平方差,设这两个数分别m、n,设m>n,即智慧数=m2-n2=(m+n)(m-n),因为m,n是正整数,因而m+n和m-n就是两个自然数.要判断一个数是否是智慧数,可以把这个数分解因数,分解成两个整数的积,看这两个数能否写成两个正整数的和与差.
解:1不能表示为两个正整数的平方差,所以1不是“智慧数”.对于大于1的奇正整数2k+1,有2k+1=(k+1)2-k2(k=1,2,…).所以大于1的奇正整数都是“智慧数”.
对于被4整除的偶数4k,有4k=(k+1)2-(k-1)2(k=2,3,…).
即大于4的被4整除的数都是“智慧数”,而4不能表示为两个正整数平方差,所以4不是“智慧数”.
对于被4除余2的数4k+2(k=0,1,2,3,…),设4k+2=x2-y2=(x+y)(x-y),其中x,y为正整数,
当x,y奇偶性相同时,(x+y)(x-y)被4整除,而4k+2不被4整除;
当x,y奇偶性相异时,(x+y)(x-y)为奇数,而4k+2为偶数,总得矛盾.
所以不存在自然数x,y使得x2-y2=4k+2.即形如4k+2的数均不为“智慧数”.
因此,在正整数列中前四个正整数只有3为“智慧数”,此后,每连续四个数中有三个“智慧数”.
因为2017=(1+3×672),4×(672+1)=2692,所以2692是第2017个“智慧数”,
所以2693是第2018个“智慧数”,2694÷4=673……2,所以不是智慧数,2695是第2019个“智慧数”,
故答案为: 2695.
-
科目: 来源: 题型:
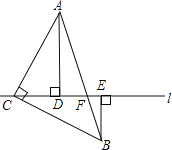
查看答案和解析>>【题目】如图,将等腰直角三角形ABC的直角顶点置于直线
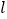 上,且过A,B两点分别作直线l的垂线,垂足分别为D,E.
上,且过A,B两点分别作直线l的垂线,垂足分别为D,E.(1)请你在图中找出一对全等三角形,并写出证明过程;
(2)若BE=3,DE=5,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组
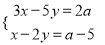 ,则下列结论中正确的是( )
,则下列结论中正确的是( )①当a=5时,方程组的解是
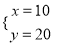 ;
;
②当x,y的值互为相反数时,a=20;③不存在一个实数a使得x=y;
④若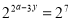 ,则a=2.
,则a=2.A. ①②③④ B. ②③ C. ②③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
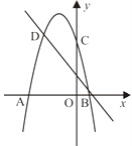
(1)求二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.

(1)求证:AE是⊙O的切线;
(2)当BC=4时求劣弧AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在《朗读者》节目的影响下,某中学开展了“好书伴我成长”读书活动.为了解5月份八年级300名学生的读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
册数
0
1
2
3
4
人数
3
13
16
17
1
关于这组数据,下列说法正确的是 ( )
A. 中位数是2 B. 众数是17 C. 平均数是3 D. 方差是2
相关试题

