搜索
【题目】已知关于x，y的方程组
，则下列结论中正确的是（ ）
①当a=5时，方程组的解是
；
②当x，y的值互为相反数时，a=20；
③不存在一个实数a使得x=y；
④若
，则a=2．
A. ①②③④ B. ②③ C. ②③④ D. ②③④
参考答案：
【答案】B
【解析】分析：①把a=5代入方程组求出解，即可做出判断；
②根据题意得到x+y=0，代入方程组求出a的值，即可做出判断；
③假如x=y，得到a无解，本选项正确；
④根据题中等式得到2a﹣3y=7，代入方程组求出a的值，即可做出判断．
详解：①把a=5代入方程组得： 
，解得： 
，本选项错误；
②由x与y互为相反数，得到：x+y=0，即y=﹣x，代入方程组得： 
，解得：a=20，本选项正确；
③若x=y，则有
，可得：a=a﹣5，矛盾，故不存在一个实数a使得x=y，本选项正确；
④方程组解得： 
，由题意得：2a﹣3y=7，把x=25﹣a，y=15﹣a代入得：2a﹣45+3a=7，解得：a=
，本选项错误．
故正确的有②③．故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图．下列三条语句：①AB∥CD，②∠B＝∠C．③∠E＝∠F．从中任选两个作为条件，另一个作为结论，编一道数学题，并说明理由。（本题满分6分）
已知：__________________________________
结论：__________________________________
理由：
-
科目： 来源： 题型：
查看答案和解析>>【题目】有许多代数恒等式可以用图形的面积来表示，如图①，它表示(2m+n)(m+n)=2m2+3mn+n2．
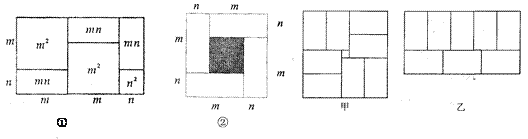
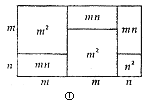
(1) 观察图②,请你写出三个代数式(m+n) 2、(m－n) 2、mn之间的等量关系是_________;
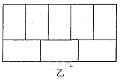
(2) 小明用8个一样大的长方形(长acm，宽bcm)拼图，拼出了如图甲、乙的两种图案：图案甲是一个正方形，图案乙是一个大的长方形：图案甲的中间留下了边长是2cm的正方形小洞．则(a+2b)2－8ab的值_______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明在学了三角形的角平分线后，遇到下列4个问题，请你帮他解决．如图，在△ABC中，∠BAC= 50°，点I是∠ABC、∠ACB平分线的交点．
问题(1)：填空：∠BIC＝_________°．
问题(2)：若点D是两条外角平分线的交点，则∠BDC＝_________°．
问题(3)：若点E是内角∠ABC、外角∠ACG的平分线的交点，则∠BEC与∠BAC的数量关系是________；
问题(4)：在问题（3）的条件下，当∠ACB等于__________°时，CE∥AB．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列等式：
12×231=132×21，
13×341=143×31，
23×352=253×32，
34×473=374×43，
62×286=682×26，
……
以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”．
（1）根据上述各式反映的规律填空，使式子成为“数字对称等式”：
①52× ＝ ×25；
② ×396＝693× ．
（2）设这类等式左边两位数的十位数字为
，个位数字为
，且2≤
≤9，写出表示“数字对称等式”一般规律的式子（含、），并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了打造区域中心城市，实现攀枝花跨越式发展，我市花城新区建设正按投资计划有序推进．花城新区建设工程部，因道路建设需要开挖土石方，计划每小时挖掘土石方540m3，现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，租赁公司提供的挖掘机有关信息如表：
（1）若租用甲、乙两种型号的挖掘机共8台，恰好完成每小时的挖掘量，则甲、乙两种型号的挖掘机各需多少台？
（2）请你设计一种方案，不仅每小时支付的租金最少，又恰好能完成每小时的挖掘量？
-
科目： 来源： 题型：
查看答案和解析>>【题目】你会求
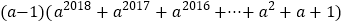的值吗?这个问题看上去很复杂，我们可以先考虑简单的情况，通过计算，探索规律：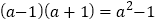
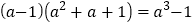
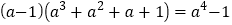
（1）由上面的规律我们可以大胆猜想，得到
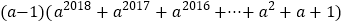=________ 利用上面的结论，求
（2）
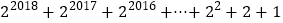的值；（3）求
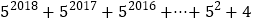的值.
相关试题
