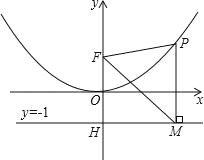
【题目】二次函数图象的顶点在原点O,经过点A(1,![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
参考答案:
【答案】(1)二次函数的解析式为y=![]() x2;(2)证明见试题解析;(3)满足条件的点P的坐标为(2
x2;(2)证明见试题解析;(3)满足条件的点P的坐标为(2![]() ,3)或(﹣2
,3)或(﹣2![]() ,3).
,3).
【解析】
试题分析:(1)根据题意可设函数的解析式为y=ax2,将点A代入函数解析式,求出a的值,继而可求得二次函数的解析式;
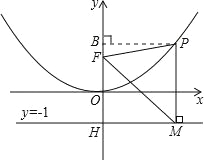
(2)过点P作PB⊥y轴于点B,利用勾股定理求出PF,表示出PM,可得PF=PM,∠PFM=∠PMF,结合平行线的性质,可得出结论;
(3)首先可得∠FMH=30°,设点P的坐标为(x,![]() x2),根据PF=PM=FM,可得关于x的方程,求出x的值即可得出答案.
x2),根据PF=PM=FM,可得关于x的方程,求出x的值即可得出答案.
试题解析:(1)∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将点A(1,![]() )代入y=ax2得:a=
)代入y=ax2得:a=![]() ,
,
∴二次函数的解析式为y=![]() x2;
x2;
(2)∵点P在抛物线y=![]() x2上,
x2上,
∴可设点P的坐标为(x,![]() x2),
x2),
过点P作PB⊥y轴于点B,则BF=|![]() x2﹣1|,PB=|x|,
x2﹣1|,PB=|x|,
∴Rt△BPF中,
PF=![]() =
=![]() x2+1,
x2+1,
∵PM⊥直线y=﹣1,
∴PM=![]() x2+1,
x2+1,
∴PF=PM,
∴∠PFM=∠PMF,
又∵PM∥y轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP;
(3)当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴![]() x2+1=4,
x2+1=4,
解得:x=±2![]() ,
,
∴![]() x2=
x2=![]() ×12=3,
×12=3,
∴满足条件的点P的坐标为(2![]() ,3)或(﹣2
,3)或(﹣2![]() ,3).
,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B,C在同一直线上,AB=4cm,AC=3cm,则B,C两点之间的距离是cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用公式法解方程x2-2=-3x时,a , b , c的值依次是( )
A.0,-2,-3
B.1,3,-2
C.1,-3,-2
D.1,-2,-3 -
科目: 来源: 题型:
查看答案和解析>>【题目】(13分)阅读材料:我们都知道
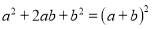 ,
,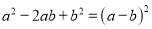
于是,
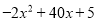
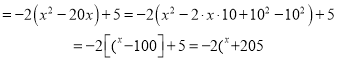
又因为
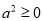 ,所以,
,所以, 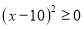 ,
, 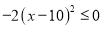 ,
, 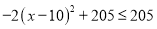
所以,
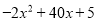 有最大值205。
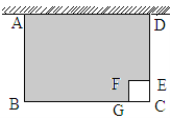
有最大值205。如图,某农户准备用长34米的铁栅栏围成一边靠墙的长方形羊圈ABCD和一个边长为1米的正方形狗屋CEFG。设AB=x米。
(1)请用含x的代数式表示BC的长(写出具体解题过程);
(2)设山羊活动范围即图中阴影部分的面积为S,试用含x的代数式表示S,并计算当x=5时S的值;
(3)试求出山羊活动范围面积S的最大值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积. 例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
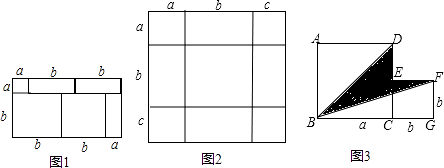
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角是它的余角的4倍,求这个角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点C是线段AB上的一点,如果线段AC=8cm,线段BC=4cm,则线段AC和BC的中点间的距离为 .
相关试题

