【题目】(13分)阅读材料:我们都知道![]() ,
,![]()
于是, ![]()
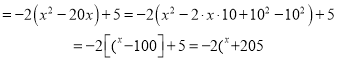
又因为![]() ,所以,
,所以, ![]() ,
, ![]() ,
, ![]()
所以, ![]() 有最大值205。
有最大值205。
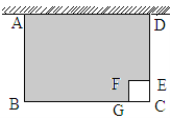
如图,某农户准备用长34米的铁栅栏围成一边靠墙的长方形羊圈ABCD和一个边长为1米的正方形狗屋CEFG。设AB=x米。
(1)请用含x的代数式表示BC的长(写出具体解题过程);
(2)设山羊活动范围即图中阴影部分的面积为S,试用含x的代数式表示S,并计算当x=5时S的值;
(3)试求出山羊活动范围面积S的最大值。
参考答案:
【答案】(1)BC=32-2x;(2)109;(3)127
【解析】试题分析:(1)根据AB+CD+BC+EF+FG=34,代入数据即可得出BC;
(2)根据阴影部分面积=长方形ABCD的面积-正方形CEFG的面积,代入数据整理即可得出结论;
(3)将S的表达式化为材料中的形式,从而可以求得所求面积的最大值.
试题解析:
解:(1)依题意得AB=DC=x,EF=FG=1,
∵AB+CD+BC+EF+FG=34,
∴2x+BC+2=34,
∴BC=32-2x ;
(2)依题意得
S=S长方形ABCD-S正方形CEFG
=x(32-x)-1
=-2x2+32x-1,
当x=5时,S=-2×5+32×5-1=109(㎡);
(3)S=-2x2+32x-1
=-2(x2-16x)-1
=-2(x2-2·x·8+82-82)-1
=-2[(x-8)2-64]-1
=-2(x-8)2+127,
又因为a2≥0,
所以(x-8)2≥0,
所以-2(x-8)2≤0,
所以-2(x-8)2+127≤127,
所以山羊活动范围面积S的最大值是127平方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B,C在同一直线上,AB=4cm,AC=3cm,则B,C两点之间的距离是cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用公式法解方程x2-2=-3x时,a , b , c的值依次是( )
A.0,-2,-3
B.1,3,-2
C.1,-3,-2
D.1,-2,-3 -
科目: 来源: 题型:
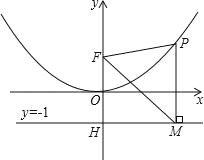
查看答案和解析>>【题目】二次函数图象的顶点在原点O,经过点A(1,
 );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积. 例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
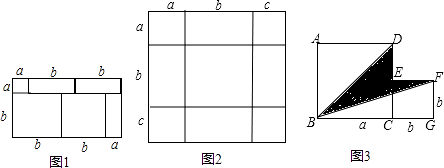
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角是它的余角的4倍,求这个角.
相关试题

