【题目】已知点C是线段AB上的一点,如果线段AC=8cm,线段BC=4cm,则线段AC和BC的中点间的距离为 .
参考答案:
【答案】4cm
【解析】解:根据题意,
①点C在线段AB外,如图,![]()
∵AB=8cm,BC=4cm,点E、F分别是线段AC、BC的中点,
∴CE= ![]() AC=
AC= ![]() (AB+BC)=
(AB+BC)= ![]() ×(8+4)=6(cm),FC=
×(8+4)=6(cm),FC= ![]() BC=2cm,
BC=2cm,
∴EF=CE﹣FC=6cm﹣2cm=4cm;
②点C在线段AB上,如图2,![]()
∵AB=8cm,BC=4cm,点E、F分别是线段AC、BC的中点,
∴CE= ![]() AC=
AC= ![]() (AB﹣BC)=2cm,FC=
(AB﹣BC)=2cm,FC= ![]() BC=2cm,
BC=2cm,
∴EF=CE+FC=2cm+2cm=4cm;
所以答案是:4cm.
【考点精析】解答此题的关键在于理解两点间的距离的相关知识,掌握同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.
-
科目: 来源: 题型:
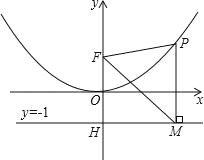
查看答案和解析>>【题目】二次函数图象的顶点在原点O,经过点A(1,
 );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积. 例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
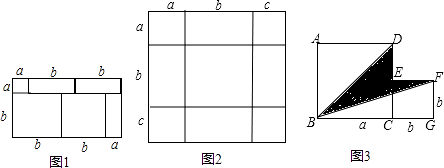
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角是它的余角的4倍,求这个角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(﹣1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )

A.8:1
B.6:1
C.5:1
D.4:1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点C是线段AB上的一点,如果线段AC=8cm,线段BC=4cm,则线段AC和BC的中点间的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:0﹣2018=_____.
相关试题

