搜索
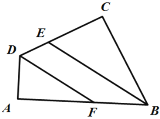
【题目】如图，四边形ABCD中，∠A=∠C=90°，BE、DF分别平分∠ABC、∠ADC，判断BE、DF是否平行，并说明理由．
参考答案：
【答案】BE∥DF，理由见解析．
【解析】
根据四边形的内角和为360°得到∠ADC+∠ABC=180°，再根据角平分线的性质得到∠ABE+∠ADF =90°，再由等量替换得到∠AFD=∠ABE，根据同位角相等两直线平行即可得到；
BE∥DF，理由如下：
证明：四边形ABCD中，∠A=∠C=90°，
∴∠ADC+∠ABC=180°，
∵BE平分∠ABC，DF平分∠ADC，
∴∠ADF=∠FDC，∠ABE=∠CBE，
∴∠ABE+∠ADF =90°，
∵∠AFD+∠ADF=90°，
∴∠AFD=∠ABE（等量替换），
∴BE∥DF（同位角相等，两直线平行）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】完全平方公式：（a±b）2＝a2±2ab+b2适当的变形，可以解决很多的数学问题．
例如：若a+b＝3，ab＝1，求a2+b2的值．
解：因为a+b＝3，ab＝1
所以（a+b）2＝9，2ab＝2
所以a2+b2+2ab＝9，2ab＝2
得a2+b2＝7
根据上面的解题思路与方法，解决下列问题：
（1）若（7﹣x）（x﹣4）＝1，求（7﹣x）2+（x﹣4）2的值；
（2）如图，点C是线段AB上的一点，以AC、BC为边向两边作正方形，设AB＝5，两正方形的面积和S1+S2＝17，求图中阴影部分面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠BAC＝90°，点D是BC上一点，将△ABD沿AD翻折后得到△AED，边AE交射线BC于点F．（友情提醒：翻折前后的两个三角形的对应边相等，对应角相等．）
（1）如图①，当AE⊥BC时，求证：DE∥AC．
（2）若
，∠BAD＝x° ．①如图②，当DE⊥BC时，求x的值；
②是否存在这样的x的值，使得△DEF中有两个角相等．若存在，并求x的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校在艺术节宣传活动中，采用了四种宣传形式：A唱歌，B舞蹈，C朗诵，D器乐．全校的每名学生都选择了一种宣传形式参与了活动，小明对同学们选用的宣传形式，进行了随机抽样调查，根据调查统计结果，绘制了如图两种不完整的统计图表：
选项
方式
百分比
A
唱歌
35%
B
舞蹈
a
C
朗诵
25%
D
器乐
30%
请结合统计图表，回答下列问题：
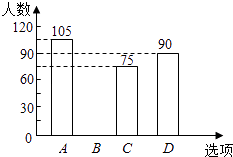
（1）本次调查的学生共人，a= ， 并将条形统计图补充完整 ；
（2）如果该校学生有2000人，请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人？
（3）学校采用调查方式让每班在A、B、C、D四种宣传形式中，随机抽取两种进行展示，请用树状图或列表法，求某班抽到的两种形式有一种是“唱歌”的概率． -
科目： 来源： 题型：
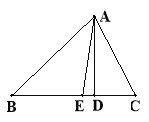
查看答案和解析>>【题目】如图，在△ABC中，AE是∠BAC的角平分线，AD是BC边上的高，且∠B ＝ 40, ∠C ＝ 60,求∠CAD、∠EAD的度数。（6分）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线
经过点
，
．
（1）求直线
的解析式；（2）若直线
与直线
相交于点
，求点
的坐标；（3）根据图象，直接写出关于
的不等式
的解集． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P1、P2（P2在P1的右侧）是y=
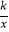（k＞0）在第一象限上的两点，点A1的坐标为（2，0）．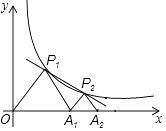
（1）填空：当点P1的横坐标逐渐增大时，△P1OA1的面积将（减小、不变、增大）
（2）若△P1OA1与△P2A1A2均为等边三角形，
①求反比例函数的解析式；
②求出点P2的坐标，并根据图象直接写在第一象限内，当x满足什么条件时，经过点P1、P2的一次函数的函数值大于反比例函数y=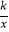 的函数值．
相关试题
