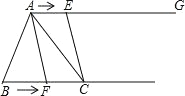
【题目】如图,在△ABC 中,BC=6cm.射线 AG∥BC,点 E 从点 A 出发沿射线 AG 以 2cm/s 的速度运动,当点 E 先出发 1s 后,点 F 也从点 B 出发沿射线 BC 以![]() cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
(1)当 t 为何值时,∠BAF<∠BAC;
(2)当 t 为何值时,AE=CF;
(3)当 t 为何值时,S△ABF+S△ACE<S△ABC.
参考答案:
【答案】(1) 0<t<![]() ;(2) t=
;(2) t= ![]() ,t=
,t= ![]() 时,AE=CF;(3) 当 0<t<
时,AE=CF;(3) 当 0<t<![]() 时,S△ABF+S△ACE<S△ABC.
时,S△ABF+S△ACE<S△ABC.
【解析】(1)根据边越长,边所对的角越大,可得答案;
(2)分类讨论:当点F在点C左侧时,点F再点C的右侧时,可得关于t的一元一次方程,根据解方程,可得答案;
(3)根据平行线间的距离相等,可得三角形的高相等,根据等高的三角形的底边越长,三角形的面积越大,可得不等式.
(1)当 BF<BC 时,∠BAF<∠BAC,
∴![]() t<6, 解得 t<
t<6, 解得 t<![]() ,
,
当 0<t<![]() 时,∠BAF<∠BAC;
时,∠BAF<∠BAC;
(2)分两种情况讨论:
①点 F 在点 C 左侧时,AE=CF,
则 2(t+1)=6﹣![]() t, 解得 t=
t, 解得 t=![]() ;
;
②当点F在点 C 的右侧时,AE=CF,
则 2(t+1)=![]() t, 解得 t=
t, 解得 t=![]() ,
,
综上所述,t=![]() ,t=
,t=![]() 时,AE=CF;
时,AE=CF;
(3)当 BF+AE<BC,S△ABF+S△ACE<S△ABC,![]() t+2(t+1)<6,解得 t<
t+2(t+1)<6,解得 t<![]() ,
,
当 0<t<![]() 时,S△ABF+S△ACE<S△ABC.
时,S△ABF+S△ACE<S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
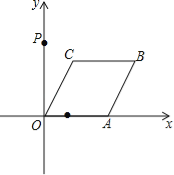
(1)点C的坐标(用含t的代数式表示);
(2)点A在运动过程中,当t为何值时,使得△OCP为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=
 x+b的图象与反比例函数y=
x+b的图象与反比例函数y= 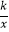 (x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当 x+b<
x+b< 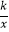 时,请直接写出x的取值范围.
时,请直接写出x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O是正方形ABCD两对角线的交点. 分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转
 角(0°<
角(0°<  <360°)得到正方形
<360°)得到正方形 ,如图2.
,如图2.①在旋转过程中,当∠
 是直角时,求
是直角时,求 的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)
的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)②若正方形ABCD的边长为1,在旋转过程中,求
 长的最大值和此时
长的最大值和此时 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,点B在x轴上,且
,点B在x轴上,且 .
. 求点B的坐标;
求点B的坐标; 求
求 的面积;
的面积; 在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
相关试题

