【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图. 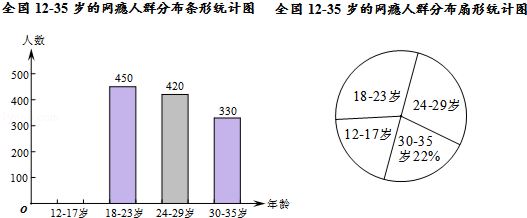
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数.
参考答案:
【答案】
(1)1500
(2)解:如图所示:
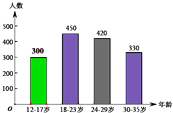
(3)108°
(4)解:其中12﹣23岁的人数 2000×50%=1000(万人)
【解析】解:(1)这次抽样调查中共调查了330÷22%=1500(人);(2)12﹣17岁的人数为1500﹣450﹣420﹣330=300(人) 补充完整,如图  ;(3)扇形统计图中18﹣23岁部分的圆心角的度数是
;(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ![]() ×360°=108°;
×360°=108°;
(1)根据30﹣35岁的人数除以所占的百分比,可得调查的人数;(2)根据有理数的减法,可得12﹣17岁的人数,根据12﹣17岁的人数,可得答案;(3)根据18﹣23岁的人数除以抽查的人数乘以360°,可得答案;(4)根据总人数乘以12﹣23岁的人数所占的百分比,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,点B在x轴上,且
,点B在x轴上,且 .
. 求点B的坐标;
求点B的坐标; 求
求 的面积;
的面积; 在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对
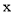 ,
, 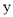 定义一种新运算
定义一种新运算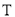 ,规定
,规定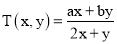 (其中
(其中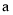 ,
, 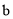 均为非零常数),这里等式右边是通常的四则运算,例:
均为非零常数),这里等式右边是通常的四则运算,例: 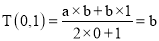 .
.已知
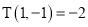 ,
, 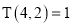 .
. (1)求
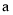 ,
, 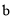 的值;
的值;(2)若关于m的不等式组
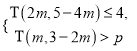 恰好有3个整数解,求实数
恰好有3个整数解,求实数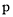 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形都是由同样大小的空心圆圈按照一定规律所组成的,其中图
 中一共有7个空心圆圈;图
中一共有7个空心圆圈;图 中一共有11个空心圆圈;图
中一共有11个空心圆圈;图 中一共有15个空心圆圈;
中一共有15个空心圆圈;
 图
图 一共应有______个空心圆圈.
一共应有______个空心圆圈. 按此规律排列下去,猜想图
按此规律排列下去,猜想图 中一共有多少个空心圆圈?用含n的代数式表示
中一共有多少个空心圆圈?用含n的代数式表示 不用说理
不用说理 .
.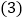 是否存在图
是否存在图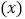 中一共有2018个空心圆圈?若存在,求出x的值;若不存在,请说明理由.
中一共有2018个空心圆圈?若存在,求出x的值;若不存在,请说明理由.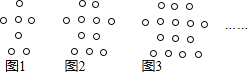
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解七年级学生期中考试数学成绩情况,从中抽取了部分学生的数学成绩进行调查,规定
 满分为100分
满分为100分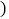 ;A等为90分
;A等为90分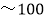 分,B等为80分
分,B等为80分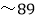 分;C等为60分
分;C等为60分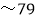 分;D等是60分以下
分;D等是60分以下 不含60分
不含60分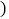 ,并根据调查结果制成如下不完整的统计图:
,并根据调查结果制成如下不完整的统计图: 本次抽查了______名七年级学生;
本次抽查了______名七年级学生; 补全条形统计图;
补全条形统计图; 求扇形统计图中表示“C等”部分的扇形的中心角度数;
求扇形统计图中表示“C等”部分的扇形的中心角度数; 结合统计图,写出两条正确的结论.
结合统计图,写出两条正确的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:请你添加一个条件_____可以得到


-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<-2.5>=-2.根据上述规定,解决下列问题:
(1)[-4.5]=______,<3.01>=____;
(2)若x为整数,且[x]+<x>=2 017,求x的值;
(3)若x,y满足方程组
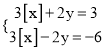 ,求x,y的取值范围.
,求x,y的取值范围.
相关试题

