【题目】 如图,点 C,F,E,B 在一条直线上, ![]() CFD =
CFD = ![]() BEA , CE = BF,DF = AE .
BEA , CE = BF,DF = AE . 
(1)求证:DF∥AE;
(2)写出 CD 与 AB 之间的关系,并证明你的结论.
参考答案:
【答案】
(1)证明:∵ ∠CFD=∠BEA ,
∴∠DFE=∠AEF,
∴DF∥AE.
(2)解:CD=AB,且 CD∥AB,理由如下:
∵CE = BF,
∴CE-EF=BF-EF,
即CF=BE,
在 ΔCDF 和 ΔBAE 中,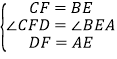
∴ΔCDF≌ΔBAE,
∴CD=BA,∠C=∠B,
∴CD∥BA.
【解析】(1)根据等角的补角相等得到∠DFE=∠AEF,再由内错角相等,两直线平行即可得证.
(2)CD=AB,且 CD∥AB,理由如下:由CE = BF得出CF=BE,再利用全等三角形的判定SAS得出ΔCDF≌ΔBAE,由全等三角形的性质得出CD=BA,
∠C=∠B,再由内错角相等,两直线平行得出CD∥BA.
【考点精析】利用对顶角和邻补角和平行线的判定对题目进行判断即可得到答案,需要熟知两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张老师计划到超市购买甲种文具100个,他到超市后发现还有乙种文具可供选择.如果调整文具的购买品种,每减少购买1个甲种文具,需增加购买2个乙种文具.设购买x个甲种文具时,需购买y个乙种文具.
(1)①当减少购买1个甲种文具时,x= ,y= ;②求y与x之间的函数表达式.
(2)已知甲种文具每个5元,乙种文具每个3元,张老师购买这两种文具共用去540元.甲、乙两种文具各购买了多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校国旗护卫队成员的身高分布如下表:
身高/cm
159
160
161
162
人数
7
10
9
9
则学校国旗护卫队成员的身高的众数和中位数分别是( )
A.160和160
B.160和160.5
C.160和161
D.161和161 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个零件的形状如图,按规定∠A= 90°,∠B、∠C 分别是 32°和 21°.某检验工人量得∠BDC= 148°,就断定这个零件不合格,试用三角形的有关知识说明零件不合格的理由.
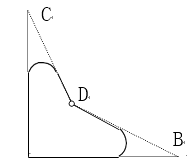
-
科目: 来源: 题型:
查看答案和解析>>【题目】折纸的思考.
【操作体验】
用一张矩形纸片折等边三角形.
第一步,对折矩形纸片
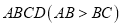 (图①),使
(图①),使 与
与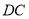 重合,得到折痕
重合,得到折痕 ,把纸片展平(图②).
,把纸片展平(图②).第二步,如图③,再一次折叠纸片,使点
 落在
落在 上的
上的 处,并使折痕经过点
处,并使折痕经过点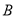 ,得到折痕
,得到折痕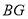 ,折出
,折出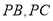 ,得到
,得到 .
.(1)说明
 是等边三角形.
是等边三角形.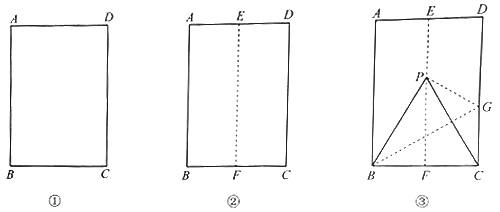
【数学思考】
(2)如图④.小明画出了图③的矩形
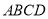 和等边三角形
和等边三角形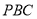 .他发现,在矩形
.他发现,在矩形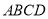 中把
中把 经过图形变化,可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.
经过图形变化,可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.(3)已知矩形一边长为3
 ,另一边长为
,另一边长为 .对于每一个确定的
.对于每一个确定的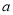 的值,在矩形中都能画出最大的等边三角形.请画出不同情形的示意图,并写出对应的
的值,在矩形中都能画出最大的等边三角形.请画出不同情形的示意图,并写出对应的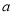 的取值范围.
的取值范围.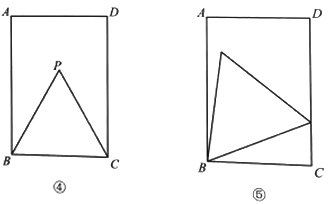
【问题解决】
(4)用一张正方形铁片剪一个直角边长分别为4
 和1
和1 的直角三角形铁片,所需正方形铁片的边长的最小值为
的直角三角形铁片,所需正方形铁片的边长的最小值为  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个数的立方根就是它本身,则这个数是________.
相关试题

