【题目】折纸的思考.
【操作体验】
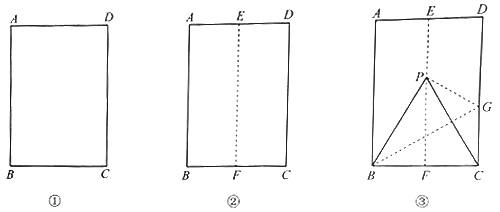
用一张矩形纸片折等边三角形.
第一步,对折矩形纸片![]() (图①),使
(图①),使![]() 与
与![]() 重合,得到折痕
重合,得到折痕![]() ,把纸片展平(图②).
,把纸片展平(图②).
第二步,如图③,再一次折叠纸片,使点![]() 落在
落在![]() 上的
上的![]() 处,并使折痕经过点
处,并使折痕经过点![]() ,得到折痕
,得到折痕![]() ,折出
,折出![]() ,得到
,得到![]() .
.
(1)说明![]() 是等边三角形.
是等边三角形.
【数学思考】
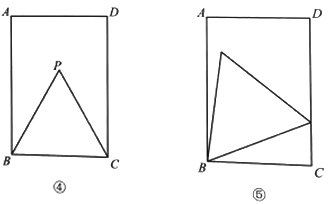
(2)如图④.小明画出了图③的矩形![]() 和等边三角形
和等边三角形![]() .他发现,在矩形
.他发现,在矩形![]() 中把
中把![]() 经过图形变化,可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.
经过图形变化,可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.
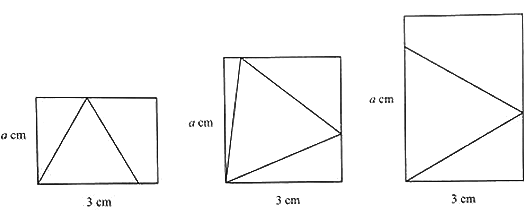
(3)已知矩形一边长为3![]() ,另一边长为
,另一边长为![]() .对于每一个确定的
.对于每一个确定的![]() 的值,在矩形中都能画出最大的等边三角形.请画出不同情形的示意图,并写出对应的
的值,在矩形中都能画出最大的等边三角形.请画出不同情形的示意图,并写出对应的![]() 的取值范围.
的取值范围.
【问题解决】
(4)用一张正方形铁片剪一个直角边长分别为4![]() 和1
和1![]() 的直角三角形铁片,所需正方形铁片的边长的最小值为
的直角三角形铁片,所需正方形铁片的边长的最小值为 ![]() .
.
参考答案:
【答案】(1)![]() 是等边三角形(2)答案见解析(3)
是等边三角形(2)答案见解析(3)![]() ,
,![]() ,
,![]() ;(4)
;(4)![]()
【解析】
试题分析:(1)由折叠的性质,重合部分的线段,角都相等可判断;
(2)根据旋转的性质和位似变换直接可做图,写出过程;
(3)根据图形,由勾股定理和等边三角形的性质求解;
(4)根据上面的规律,由勾股定理和等边三角形直接可求解.
试题解析:(1)由折叠,![]() ,
,
因此,![]() 是等边三角形.
是等边三角形.
(2)本题答案不惟一,下列解法供参考.例如,
如图,以点![]() 为中心,在矩形
为中心,在矩形![]() 中把
中把![]() 逆时针方向旋转适当的角度,得到
逆时针方向旋转适当的角度,得到![]() ;
;
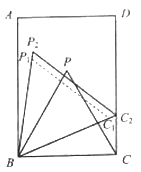
再以点![]() 为位似中心,将
为位似中心,将![]() 放大,使点
放大,使点![]() 的对应点
的对应点![]() 落在
落在![]() 上,得到
上,得到![]() .
.
(3)本题答案不惟一,下列解法供参考,例如,
![]()
![]()
![]()
(4)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校国旗护卫队成员的身高分布如下表:
身高/cm
159
160
161
162
人数
7
10
9
9
则学校国旗护卫队成员的身高的众数和中位数分别是( )
A.160和160
B.160和160.5
C.160和161
D.161和161 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个零件的形状如图,按规定∠A= 90°,∠B、∠C 分别是 32°和 21°.某检验工人量得∠BDC= 148°,就断定这个零件不合格,试用三角形的有关知识说明零件不合格的理由.
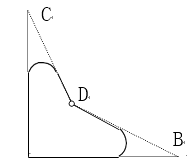
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,点 C,F,E,B 在一条直线上,
 CFD =
CFD =  BEA , CE = BF,DF = AE .
BEA , CE = BF,DF = AE . 
(1)求证:DF∥AE;
(2)写出 CD 与 AB 之间的关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个数的立方根就是它本身,则这个数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,∠ABC,∠BCD 的角平分线交 AD 于 E 点,且 E 在 AD 上,CE 交 BA 的延长线于 F 点.

(1)试问 BE 与 CF 互相垂直吗?若垂直,请说明理由;
(2)若 CD=3,AB=4,求 BC 的长 .
相关试题

