【题目】如图,在平面直角坐标系中有一正方形AOBC,反比例函数 ![]() 经过正方形AOBC对角线的交点,半径为(4﹣2
经过正方形AOBC对角线的交点,半径为(4﹣2 ![]() )的圆内切于△ABC,则k的值为 .
)的圆内切于△ABC,则k的值为 . 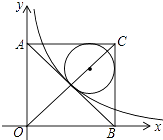
参考答案:
【答案】4
【解析】解:设正方形对角线交点为D,过点D作DM⊥AO于点M,DN⊥BO于点N; 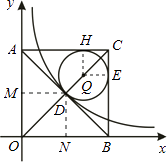
设圆心为Q,切点为H、E,连接QH、QE.
∵在正方形AOBC中,反比例函数 ![]() 经过正方形AOBC对角线的交点,
经过正方形AOBC对角线的交点,
∴AD=BD=DO=CD,NO=DN,HQ=QE,HC=CE,
QH⊥AC,QE⊥BC,∠ACB=90°,
∴四边形HQEC是正方形,
∵半径为(4﹣2 ![]() )的圆内切于△ABC,
)的圆内切于△ABC,
∴DO=CD,
∵HQ2+HC2=QC2 ,
∴2HQ2=QC2=2×(4﹣2 ![]() )2 ,
)2 ,
∴QC2=48﹣32 ![]() =(4
=(4 ![]() ﹣4)2 ,
﹣4)2 ,
∴QC=4 ![]() ﹣4,
﹣4,
∴CD=4 ![]() ﹣4+(4﹣2
﹣4+(4﹣2 ![]() )=2
)=2 ![]() ,
,
∴DO=2 ![]() ,
,
∵NO2+DN2=DO2=(2 ![]() )2=8,
)2=8,
∴2NO2=8,
∴NO2=4,
∴DN×NO=4,
即:xy=k=4.
所以答案是:4.
【考点精析】根据题目的已知条件,利用正方形的性质和三角形的内切圆与内心的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了二次根式的相关运算后,我们发现一些含有根号的式子可以表示成另一个式子的平方,如:
3+2
 =2+2
=2+2 +1=(
+1=( )2+2
)2+2 +1=(
+1=( +1)2;
+1)2;5+2
 =2+2
=2+2 +3=(
+3=( )2+2×
)2+2× ×
× +(
+( )2=(
)2=( +
+ )2
)2(1)请仿照上面式子的变化过程,把下列各式化成另一个式子的平方的形式:
①4+2
 ;②6+4
;②6+4
(2)若a+4
 =(m+n
=(m+n )2,且a,m,n都是正整数,试求a的值.
)2,且a,m,n都是正整数,试求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC﹣CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.

(1)当2<m≤8时,AP=,AQ=.(用m的代数式表示)
(2)当线段FG长度达到最大时,求m的值;
(3)在点P,Q整个运动过程中, ①当m为何值时,⊙O与△ABC的一边相切?
②直接写出点F所经过的路径长是.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】填在如图各正方形中的四个数之间都有相同的规律,根据这种规律,m的值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B分别是反比例函数y=
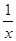 (x>0),y=
(x>0),y= 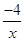 (x<0)的图象上的点,且,∠AOB=90°,则
(x<0)的图象上的点,且,∠AOB=90°,则 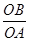 的值为( )
的值为( ) 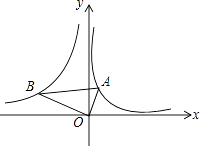
A.4
B.
C.2
D.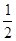
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其它四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了尚不完整的频数分布表:
类别
频数(人数)
频率
文学
m
0.42
艺术
22
0.11
科普
66
n
其他
28
合计
1
(1)表中m= , n=;
(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最少?
(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
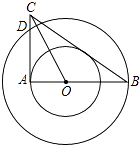
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由.
(3)若AB=8,BC=10,求大圆与小圆围成的圆环的面积.
相关试题

