【题目】如图,在平面直角坐标系,A(a,0),B(b,0),C(﹣1,2),且|2a+b+1|+(a+2b﹣4)2=0.
(1)求a,b的值;
(2)①在x轴的正半轴上存在一点M,使S△COM=![]() △ABC的面积,求出点M的坐标;
△ABC的面积,求出点M的坐标;
②在坐标轴的其他位置是否存在点M,使△COM的面积=![]() △ABC的面积仍然成立?若存在,请直接写出符合条件的点M的坐标为 .
△ABC的面积仍然成立?若存在,请直接写出符合条件的点M的坐标为 .

参考答案:
【答案】(1)a=﹣2,b=3(2)①M(![]() ,0)②(﹣
,0)②(﹣![]() ,0),(0,5),(0,﹣5).
,0),(0,5),(0,﹣5).
【解析】试题分析:(1)由绝对值和偶次方的非负性列出二元一次方程组,解方程组即可得出a,b的值,
(2)①先求出△ABC的面积,再利用△COM的面积是△ABC面积的![]() ,求出点M的坐标.
,求出点M的坐标.
②利用△COM的面积是△ABC面积的![]() ,分别求出M在x轴负半轴上的坐标和在y轴上的坐标即可.
,分别求出M在x轴负半轴上的坐标和在y轴上的坐标即可.
解:(1)∵|2a+b+1|+(a+2b﹣4)2=0,
又∵|2a+b+1|和(a+2b﹣4)2都是非负数,
所以得![]() ,
,
解方程组得,![]() ,
,
∴a=﹣2,b=3.
(2)①由(1)得A,B点的坐标为A(﹣2,0),B(3,0),|AB|=5.
∵C(﹣1,2),
∴△ABC的AB边上的高是2,
∴![]() .
.
要使△COM的面积是△ABC面积的![]() ,而C点不变,即三角形的高不变,M点在x轴的正半轴上,只需使
,而C点不变,即三角形的高不变,M点在x轴的正半轴上,只需使![]() .
.
此时![]() .
.
∴M点的坐标为![]()
②由①中![]() 的对称点得
的对称点得![]() ,
,
当M在y轴上时,△COM的高为1,
∵△COM的面积=![]() △ABC的面积,
△ABC的面积,
∴![]() |OM|×1=
|OM|×1=![]()
∴OM=±5,
∴M2(0,5)M3(0,﹣5).
故答案为:(﹣![]() ,0),(0,5),(0,﹣5).
,0),(0,5),(0,﹣5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB为等腰三角形,顶点A的坐标(2,
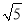 ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,请你求出点O′的坐标.
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,请你求出点O′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣4ax+3a(a>0),与y轴交于点A,在x轴的正半轴上取一点B,使OB=2OA,抛物线的对称轴与抛物线交于点C,与x轴交于点D,与直线AB交于点E,连接BC.
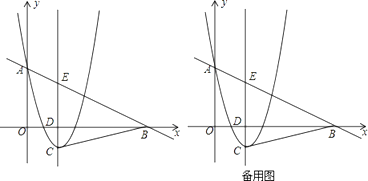
(1)求点B,C的坐标(用含a的代数式表示);
(2)若△BCD与△BDE相似,求a的值;
(3)连接OE,记△OBE的外心为M,点M到直线AB的距离记为h,请探究h的值是否会随着a的变化而变化?如果变化,请写出h的取值范围;如果不变,请求出h的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC=3cm,AC=4cm,D是AB的中点,若以点C为圆心,以3cm长为半径作⊙C,则下列选项中的点在⊙C外的是( )

A.点A
B.点B
C.点C
D.点D -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )

A.始终不变
B.先减小后增大
C.一直变大
D.一直变小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8 …,顶点依次为A1,A2,A3,A4,A5,…,则顶点A55的坐标是( )

A. (13,13) B. (-13,-13) C. (-14,-14) D. (14,14)
-
科目: 来源: 题型:
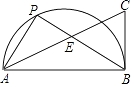
查看答案和解析>>【题目】如图,P是AB为直径的半圆周上一点,点C在∠PAB的平分线上,且CB⊥AB于B,PB交AC于E,若AB=4,BE=2,则PE的长为 .
相关试题

