【题目】如图,△AOB为等腰三角形,顶点A的坐标(2, ![]() ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,请你求出点O′的坐标.
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,请你求出点O′的坐标.

参考答案:
【答案】
【解析】试题分析:过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,根据点A的坐标求出OC、AC,再利用勾股定理列式计算求出OA,根据等腰三角形三线合一的性质求出OB,根据旋转的性质可得BO′=OB,∠A′BO′=∠ABO,然后解直角三角形求出O′D、BD,再求出OD,然后写出点O′的坐标即可.
解:如图,过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D.
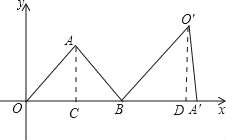
∵A(2,![]() ),
),
∴OC=2,AC=![]() ,
,
由勾股定理得,OA=![]() =3,
=3,
∵△AOB为等腰三角形,OB是底边,
∴OB=2OC=2×2=4,
由cos∠ABC=![]() =
=![]()
∴![]() =
=![]() ,
,
∴BD=![]()
∴O′D=![]() =
=![]() ,
,
∴OD=OB+BD=4+![]() =
=![]() ,
,
∴点O′的坐标为(![]() ,
,![]() ),
),
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B两个村庄的坐标分别为(2,2)、(7,4),一辆汽车从原点O出发,在x轴上行驶.
(1)汽车行驶到什么位置时离村庄A最近?写出此位置的坐标.
(2)汽车行驶到什么位置时离村庄B最近?写出此位置的坐标.
(3)请在图中画出汽车到两村庄的距离和最短的位置,并求出此最短的距离和.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一些相同的房间需要粉刷墙面,一天3名师傅去粉刷8个房间,结果其中有40㎡墙面未来得及刷;同样时间内5名徒弟粉刷了9个房间的墙面,每名师傅比徒弟一天多刷30㎡墙面.
(1)求每个房间需要粉刷的墙面面积;
(2)张老板现有36个这样的房间需要粉刷,若请1名师傅带2名徒弟去,需几天完成?
(3)已知每名师傅、徒弟每天的工资分别是85元、65元,张老板要求在3天内(包括3天)完成36个房间的粉刷,问如何在这8人中雇用人员(不一定8人全部雇用),才合算呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,过点A作⊙O的切线与直径CD的延长线交于点E,已知AE=AC.
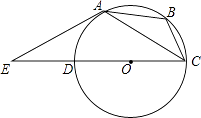
(1)求∠B的度数;
(2)若ED=1,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣4ax+3a(a>0),与y轴交于点A,在x轴的正半轴上取一点B,使OB=2OA,抛物线的对称轴与抛物线交于点C,与x轴交于点D,与直线AB交于点E,连接BC.
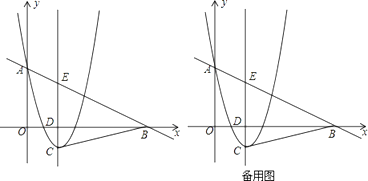
(1)求点B,C的坐标(用含a的代数式表示);
(2)若△BCD与△BDE相似,求a的值;
(3)连接OE,记△OBE的外心为M,点M到直线AB的距离记为h,请探究h的值是否会随着a的变化而变化?如果变化,请写出h的取值范围;如果不变,请求出h的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC=3cm,AC=4cm,D是AB的中点,若以点C为圆心,以3cm长为半径作⊙C,则下列选项中的点在⊙C外的是( )

A.点A
B.点B
C.点C
D.点D -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系,A(a,0),B(b,0),C(﹣1,2),且|2a+b+1|+(a+2b﹣4)2=0.
(1)求a,b的值;
(2)①在x轴的正半轴上存在一点M,使S△COM=
 △ABC的面积,求出点M的坐标;
△ABC的面积,求出点M的坐标;②在坐标轴的其他位置是否存在点M,使△COM的面积=
 △ABC的面积仍然成立?若存在,请直接写出符合条件的点M的坐标为 .
△ABC的面积仍然成立?若存在,请直接写出符合条件的点M的坐标为 .
相关试题

