【题目】如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y= ![]() x于点B1 , B2 , 过点B2作y轴的平行线交直线y=x于点A2 , 过点A2作x轴的平行线交直线y=
x于点B1 , B2 , 过点B2作y轴的平行线交直线y=x于点A2 , 过点A2作x轴的平行线交直线y= ![]() x于点B3 , …,按照此规律进行下去,则点An的横坐标为 .
x于点B3 , …,按照此规律进行下去,则点An的横坐标为 . 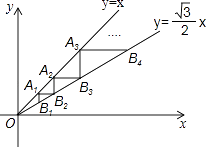
参考答案:
【答案】![]()
【解析】解:∵AnBn+1∥x轴,
∴tan∠AnBn+1Bn= ![]() .
.
当x=1时,y= ![]() x=
x= ![]() ,
,
∴点B1的坐标为(1, ![]() ),
),
∴A1B1=1﹣ ![]() ,A1B2=
,A1B2= ![]() =
= ![]() ﹣1.
﹣1.
∵1+A1B2= ![]() ,
,
∴点A2的坐标为( ![]() ,
, ![]() ),点B2的坐标为(
),点B2的坐标为( ![]() ,1),
,1),
∴A2B2= ![]() ﹣1,A2B3=
﹣1,A2B3= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴点A3的坐标为( ![]() ,
, ![]() ),点B3的坐标为(
),点B3的坐标为( ![]() ,
, ![]() ).
).
同理,可得:点An的坐标为( ![]() ,
, ![]() ).
).
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为 .
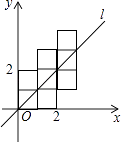
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
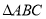 中,
中,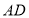 是
是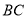 边上的中线,点
边上的中线,点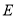 是
是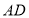 的中点;过点
的中点;过点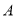 作
作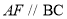 ,交
,交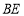 的延长线于
的延长线于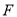 ,连接
,连接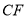 .
.(1)求证:四边形
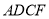 是平行四边形;
是平行四边形;(2)当
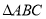 分别满足什么条件时,四边形
分别满足什么条件时,四边形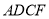 是菱形;四边形
是菱形;四边形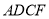 是矩形,并说明理由.
是矩形,并说明理由.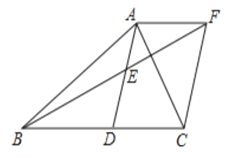
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是米.
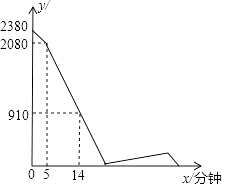
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
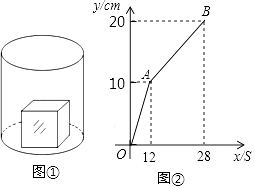
(1)正方体的棱长为cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2=
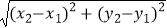 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x=
他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x= 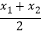 ,y=
,y= 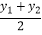 .
.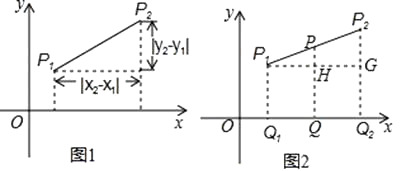
(1)请你帮小明写出中点坐标公式的证明过程;
(2)①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;
②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标:;
(3)如图3,点P(2,n)在函数y= x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.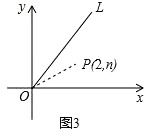
相关试题

