【题目】如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.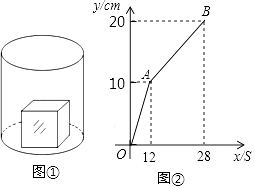
(1)正方体的棱长为cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
参考答案:
【答案】
(1)由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内高度变化趋势改变,故正方体的棱长为10cm;故答案为:10;
(2)解:设线段AB对应的函数解析式为:y=kx+b,
∵图象过A(12,10),B(28,20),
∴ ![]() ,
,
解得: ![]() ,
,
∴线段AB对应的解析式为:y= ![]() x+
x+ ![]() (12≤x≤28);
(12≤x≤28);
(3)解:∵28﹣12=16(s),
∴没有立方体时,水面上升10cm,所用时间为:16秒,
∵前12秒由立方体的存在,导致水面上升速度加快了4秒,
∴将正方体铁块取出,经过4秒恰好将此水槽注满.
【解析】(1)由图像可知点A是折点,坐标对应的水槽内水面的高度就等于小正方体的棱长;(2)AB段端点坐标均已知,利用待定系数法即可求出;(3)由图像可知,正方体棱长等于整个圆柱高度的一半,所用时间少下半部分少用4分钟,就是因为正方体的存在少用了,因此取出正方体后,经过4秒恰好将水槽注满.
-
科目: 来源: 题型:
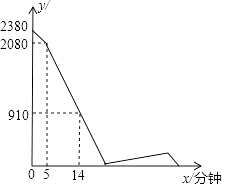
查看答案和解析>>【题目】A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y=
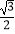 x于点B1 , B2 , 过点B2作y轴的平行线交直线y=x于点A2 , 过点A2作x轴的平行线交直线y=
x于点B1 , B2 , 过点B2作y轴的平行线交直线y=x于点A2 , 过点A2作x轴的平行线交直线y= 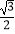 x于点B3 , …,按照此规律进行下去,则点An的横坐标为 .
x于点B3 , …,按照此规律进行下去,则点An的横坐标为 . 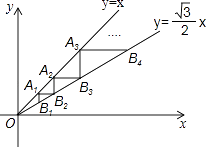
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
-
科目: 来源: 题型:
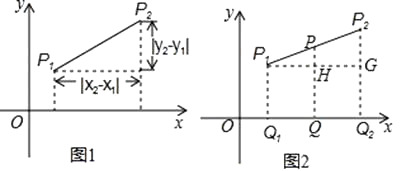
查看答案和解析>>【题目】小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2=
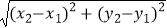 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x=
他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x= 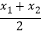 ,y=
,y= 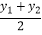 .
.
(1)请你帮小明写出中点坐标公式的证明过程;
(2)①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;
②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标:;
(3)如图3,点P(2,n)在函数y= x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.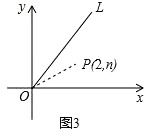
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

相关试题

