【题目】自定义:在一个图形上画一条直线,若这条直线既平分该图形的面积,又平分该图形的周长,我们称这条直线为这个图形的“等分积周线”.
(1)如图1,已知△ABC,AC≠BC,过点C能否画出△ABC的一条“等分积周线”?若能,说出确定的方法,若不能,请说明理由.
(2)如图2,在四边形ABCD中,∠B=∠C=90°,EF垂直平分AD,垂足为F,交BC于点E,已知AB=3,BC=8,CD=5.求证:直线EF为四边形ABCD的“等分积周线”;
(3)如图3,在△ABC中,AB=BC=6,AC=8,请你画出△ABC的一条“等分积周线”EF(要求:直线EF不过△ABC的顶点,交边AC于点F,交边BC于点E),并说明EF为“等分积周线”的理由.

参考答案:
【答案】(1)不能,理由见解析;(2)见解析;(3)见解析
【解析】
(1)若直线CD平分△ABC的面积,那么S△ADC=S△DBC,得出AC≠BC,进而得出答案;
(2)根据勾股定理可得出:AB2+BE2=CE2+DC2,进而得出BE=5,CE=3,进而得出周长与面积分别相等得出答案即可;
(3)在AC上取一点F,使得FC=AB=6,在BC上取一点E,使得BE=2,作直线EF,则EF是△ABC的等分积周线,结合全等三角形的判定与性质得出答案.
(1)不能,

理由:如答图1,若直线CD平分△ABC的面积,那么S△ADC=S△DBC,
∴AD=BD,
∵AC≠BC,
∴AD+AC≠BD+BC,
∴过点C不能画出一条“等分积周线”
(2)如答图2,连接AE、DE,设BE=x,
∵EF垂直平分AD,∴AE=DE,AF=DF,S△AEF=S△DEF,

∵∠B=∠C=90°,AB=3,BC=8,CD=5,
∴Rt△ABE和Rt△DCE中,根据勾股定理可得出:
AB2+BE2=CE2+DC2,即32+x2=(8-x)2+52,
解得:x=5,所以BE=5,CE=3,
∴AB+BE=CE+DC,
S△ABE=S△DCE,
∴S四边形ABEF=S△ABE+S△AEF,

S四边形DCEF=S△DEF+S△DCE,
∴S四边形ABEF=S四边形DCEF,
AF+AB+BE=DF+EC+DC,
∴直线EF为四边形ABCD的“等分积周线”;
(3)如答图3,在AC上取一点F,使得FC=AB=6,在BC上取一点E,使得BE=2,
作直线EF,则EF是△ABC的等分积周线,
理由:由作图可得:AF=AC-FC=8-6=2,在CB上取一点G,使得CG=AF=2,则有AB+AF=CF+CG,
∵AB=BC,
∴∠A=∠C,
在△ABF和△CFG中,

 ,
,
∴△ABF≌△CFG(SAS),
∴S△ABF=S△CFG,
又易得BE=EG=2,
∴S△BFE=S△EFG,
∴S△EFC=S四边形ABEF,
AF+AB+BE=CE+CF=10,
∴EF是△ABC的等分积周线,
若如答图4,当BM=2cm,AN=6cm时,直线MN也是△ABC的等分积周线.(其实是同一条)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=5cm,BC=3cm,AC=4cm,若动点P从点C开始,按照C→A→B的路径运动,且运动速度为每秒2cm,设出发的时间为t秒.
(1)请判断△ABC的形状,说明理由
(2)当t为何值时,△BCP是以BC为腰的等腰三角形,求出t的值
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒1cm,若P、Q两点同时出发, 当P、Q中有一点到达终点时,另一点也停止运动,当t为何值时,P、Q两点之间的距离为
 ,直接写出t的值.
,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,平行四边形
 的两条对角线相交于点
的两条对角线相交于点 ,
, 是
是 的中点,过点
的中点,过点 作
作 的平行线,交
的平行线,交 的延长线于点
的延长线于点 ,连结
,连结 .
.
 求证:
求证: ;
; 当平行四边形
当平行四边形 满足什么条件时,四边形
满足什么条件时,四边形 是菱形?证明你的结论.
是菱形?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】情境观察
将矩形
 纸片沿对角线
纸片沿对角线 剪开,得到
剪开,得到 和
和 ,如图
,如图 所示.将
所示.将 的顶点
的顶点 与点
与点 重合,并绕点
重合,并绕点 按逆时针方向旋转,使点
按逆时针方向旋转,使点 、
、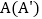 、
、 在同一条直线上,如图
在同一条直线上,如图 所示.
所示.观察图
 可知:与
可知:与 相等的线段是________,
相等的线段是________, ________°.
________°.
问题探究
如图
 ,
, 中,
中, 于点
于点 ,以
,以 为直角顶点,分别以
为直角顶点,分别以 、
、 为直角边,向
为直角边,向 外作等腰
外作等腰 和等腰
和等腰 ,过点
,过点 、
、 作射线
作射线 的垂线,垂足分别为
的垂线,垂足分别为 、
、 .试探究
.试探究 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.拓展延伸

如图
 ,
, 中,
中, 于点
于点 ,分别以
,分别以 、
、 为一边向
为一边向 外作矩形
外作矩形 和矩形
和矩形 ,射线
,射线 交
交 于点
于点 .若
.若 ,
, ,试探究
,试探究 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC、∠ACB的平分线交于点O,若∠A=40°,则∠BOC的度数为( )

A.40°B.80°C.100°D.110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,过B作BE⊥AD于E,过E作EF∥AC交AB于F,则下列结论:(1)AF=FE,(2)FE=FB,(3)FE=BE,(4)AF=BF,(5)BE =BF,成立的有( )

A.1 个B.2 个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中, ,
, ,
, .如果点
.如果点 由
由 出发沿
出发沿 方向点
方向点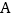 匀速运动,同时点
匀速运动,同时点 由
由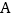 出发沿
出发沿 方向向点
方向向点 匀速运动,它们的速度均为
匀速运动,它们的速度均为 .连接
.连接 ,设运动的时间为
,设运动的时间为 (单位:
(单位: )
) .解答下列问题:
.解答下列问题:
 当
当 为何值时
为何值时 平行于
平行于 ;
; 当
当 为何值时,
为何值时, 与
与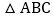 相似?
相似? 是否存在某时刻
是否存在某时刻 ,使线段
,使线段 恰好把
恰好把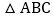 的周长平分?若存在,求出此时
的周长平分?若存在,求出此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 是否存在某时刻
是否存在某时刻 ,使线段
,使线段 恰好把
恰好把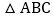 的面积平分?若存在,求出此时
的面积平分?若存在,求出此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

