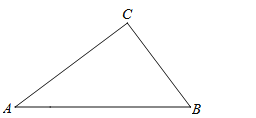
【题目】如图，△ABC中，AB=5cm，BC=3cm，AC=4cm，若动点P从点C开始，按照C→A→B的路径运动，且运动速度为每秒2cm，设出发的时间为t秒.

（1）请判断△ABC的形状，说明理由

（2）当t为何值时，△BCP是以BC为腰的等腰三角形，求出t的值

（3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒1cm，若P、Q两点同时出发， 当P、Q中有一点到达终点时，另一点也停止运动，当t为何值时，P、Q两点之间的距离为，直接写出t的值.

参考答案：

【答案】（1）△ABC是直角三角形，理由见解析；（2）t=1.5或2.7或3；（3）当t为1秒或秒时，P、Q两点之间的距离为．

【解析】

（1）直接利用勾股定的逆定理得出△ABC是直角三角形；
（2）由于动点P从点C开始，按C→A→B的路径运动，故应分点P在AC上与AB上两种情况进行讨论；
（3）当P、Q两点之间的距离为时，分四种情况讨论：点P在AC上，点Q在BC上；点P、Q均在AB上运动，且点P在点Q的左侧；点P、Q均在AB上运动，且点P在点Q的右侧；点P在AB上，点Q在BC上，分别求得t的值并检验即可．

（1）△ABC是直角三角形．
∵AB=5，BC=3，AC=4，
∴AC2+BC2=25=AB2，
∴△ABC是直角三角形；
（2）如图，当点P在AC上时，CP=CB=3，则t=3÷2=1.5秒；

如图，当点P在AB上时，分两种情况：

若BP=BC=3，则AP=2，
故t=（4+2）÷2=3秒；
若CP=CB=3，作CM⊥AB于M，则×AB×MC=×BC×AC，
×5×MC=×3×4，
解得CM=2.4，
∴由勾股定理可得PM=BM=1.8，即BP=3.6，
∴AP=1.4，
故t=（4+1.4）÷2=2.7秒．
综上所述，当t=1.5、3或2.7 时，△BCP是以BC为腰的等腰三角形．
故答案为：t=1.5或2.7或3；

（3）①如图，当点P在AC上，点Q在BC上运动时（0≤t≤2），
由勾股定理可得：（2t）2+t2=5，
解得t=1；

②如图，当点P、Q均在AB上运动，且点P在点Q的左侧时（3≤t＜4），
由题可得：12-2t-t=，
解得t= ；

③当点P、Q均在AB上运动，且点P在点Q的右侧时（4＜t≤4.5），
由题可得：2t+t-12=，
解得t=，
∵t=＞4.5，
∴不成立，舍去．
④当点P在AB上，点Q在BC上时，PQ的长不合题意；
综上所述，当t为1秒或秒时，P、Q两点之间的距离为．

关闭