搜索
【题目】如图，在△ABC中，∠ABC、∠ACB的平分线交于点O，若∠A=40°，则∠BOC的度数为（ ）
A.40°B.80°C.100°D.110°
参考答案：
【答案】D
【解析】
先根据BO平分∠ABC，CO平分∠ACB，可得∠1=
∠ABC，∠2=∠ACB，再根据三角形内角和定理计算出∠ABC+∠ACB的度数，进而得到∠1+∠2，再根据三角形内角和定理即可算出∠BOC的度数．
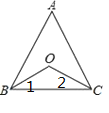
解：∵∠A=40°，
∴∠ABC+∠ACB=140°.
∵BO平分∠ABC，CO平分∠ACB，
∴∠1= ∠ABC，∠2=∠ACB，
∴∠1+∠2=（∠ABC+∠ACB ）= 
140°=70°，
∵∠BOC+∠1+∠2=180°，
∴∠BOC=180°-70°=110°.
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，平行四边形
的两条对角线相交于点
，
是
的中点，过点
作
的平行线，交
的延长线于点
，连结
．
求证：
；
当平行四边形满足什么条件时，四边形
是菱形？证明你的结论． -
科目： 来源： 题型：
查看答案和解析>>【题目】情境观察
将矩形
纸片沿对角线
剪开，得到
和
，如图
所示．将的顶点
与点
重合，并绕点按逆时针方向旋转，使点
、
、
在同一条直线上，如图
所示．观察图
可知：与
相等的线段是________，
________°．
问题探究
如图
，中，
于点
，以为直角顶点，分别以
、为直角边，向外作等腰
和等腰
，过点
、
作射线
的垂线，垂足分别为
、
．试探究
与
之间的数量关系，并证明你的结论．拓展延伸
如图
，中，于点，分别以、为一边向外作矩形
和矩形
，射线交
于点
．若
，
，试探究
与
之间的数量关系，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】自定义：在一个图形上画一条直线，若这条直线既平分该图形的面积，又平分该图形的周长，我们称这条直线为这个图形的“等分积周线”.
（1）如图1，已知△ABC，AC≠BC，过点C能否画出△ABC的一条“等分积周线”？若能，说出确定的方法，若不能，请说明理由.
（2）如图2，在四边形ABCD中，∠B=∠C=90°，EF垂直平分AD，垂足为F，交BC于点E，已知AB=3，BC=8，CD=5.求证：直线EF为四边形ABCD的“等分积周线”；
（3）如图3，在△ABC中，AB=BC=6，AC=8，请你画出△ABC的一条“等分积周线”EF（要求：直线EF不过△ABC的顶点，交边AC于点F，交边BC于点E）,并说明EF为“等分积周线”的理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD平分∠BAC，过B作BE⊥AD于E，过E作EF∥AC交AB于F，则下列结论：（1）AF=FE,（2）FE=FB,（3）FE=BE,（4）AF=BF,（5）BE =BF，成立的有（ ）
A.1 个B.2 个C.3个D.4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知
中，
，
，
．如果点
由
出发沿
方向点
匀速运动，同时点
由出发沿
方向向点
匀速运动，它们的速度均为
．连接
，设运动的时间为
（单位：
）
．解答下列问题：
当为何值时平行于
；
当为何值时，
与
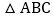相似？
是否存在某时刻，使线段恰好把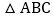的周长平分？若存在，求出此时的值；若不存在，请说明理由．
是否存在某时刻，使线段恰好把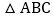的面积平分？若存在，求出此时的值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．
（1）在图中的点上标出相应字母A、B、C，并求出△ABC的面积；
（2）在图中作出△ABC关于y轴的对称图形△A1B1C1；
（3）写出点A1，B1，C1的坐标．
相关试题
