【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() .如果点
.如果点![]() 由
由![]() 出发沿
出发沿![]() 方向点
方向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由
由![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .连接
.连接![]() ,设运动的时间为
,设运动的时间为![]() (单位:
(单位:![]() )
)![]() .解答下列问题:
.解答下列问题:

![]() 当
当![]() 为何值时
为何值时![]() 平行于
平行于![]() ;
;
![]() 当
当![]() 为何值时,
为何值时,![]() 与
与![]() 相似?
相似?
![]() 是否存在某时刻
是否存在某时刻![]() ,使线段
,使线段![]() 恰好把
恰好把![]() 的周长平分?若存在,求出此时
的周长平分?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
![]() 是否存在某时刻
是否存在某时刻![]() ,使线段
,使线段![]() 恰好把
恰好把![]() 的面积平分?若存在,求出此时
的面积平分?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)当![]() 时
时![]() ;
; ![]() 当
当![]() 为
为![]() 或
或![]() 时
时![]() 和
和![]() 相似;
相似; ![]() 不存在.理由见解析;
不存在.理由见解析; ![]() 存在,当
存在,当![]() 时,线段
时,线段![]() 恰好把
恰好把![]() 的面积平分.
的面积平分.
【解析】
(1)可求得BC=6,且PB=AQ=2t,AP=10-2t,当PQ∥BC时,可得![]() =
=![]() ,代入可得到关于t的方程,可求得t;
,代入可得到关于t的方程,可求得t;
(2)分PQ⊥AC和PQ⊥AB,再利用相似得到对应线段的比相等,可得到关于t的方程,代入分别求得t即可;
(3)周长相等,即AP+AQ=PB+BC+CQ,代入可得到关于t的方程,可求得t的值;
(4)过P作PD⊥AC于点D,则PD∥BC,则![]() =
=![]() ,可用t表示出PD,进一步可表示出其面积,令其为△ABC面积的一半即可,可求出t的值,注意结合t的取值范围进行取舍.
,可用t表示出PD,进一步可表示出其面积,令其为△ABC面积的一半即可,可求出t的值,注意结合t的取值范围进行取舍.
解:∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 、
、![]() 的运动速度为
的运动速度为![]() ,
,
∴![]() ,则
,则![]() ,
,
![]() 当
当![]() 时,则
时,则![]() ,即
,即![]() ,解得
,解得![]() ,
,
即当![]() 时
时![]() ;
;
![]() ∵
∵![]() 为直角三角形,
为直角三角形,
∴当![]() 和
和![]() 相似时,必有一个角为直角,
相似时,必有一个角为直角,
当![]() 时,则
时,则![]() ,由
,由![]() 可知
可知![]() ,
,
当![]() 时,则
时,则![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴当![]() 为
为![]() 或
或![]() 时
时![]() 和
和![]() 相似;
相似;
 不存在.理由如下:
不存在.理由如下:
当线段![]() 恰好把
恰好把![]() 的周长平分时,则有
的周长平分时,则有![]() ,
,
即![]() ,整理得
,整理得![]() ,显然不成立,
,显然不成立,
∴不存在使![]() 把
把![]() 周长平分的
周长平分的![]() ;
;
![]() 存在.
存在.
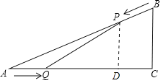
如图,过![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() ,
,
且![]() ,
,
当线段![]() 恰好把
恰好把![]() 的面积平分时,则有
的面积平分时,则有![]() ,
,
即![]() ,整理可得
,整理可得![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
∴当时,线段
![]() 恰好把
恰好把![]() 的面积平分.
的面积平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自定义:在一个图形上画一条直线,若这条直线既平分该图形的面积,又平分该图形的周长,我们称这条直线为这个图形的“等分积周线”.
(1)如图1,已知△ABC,AC≠BC,过点C能否画出△ABC的一条“等分积周线”?若能,说出确定的方法,若不能,请说明理由.
(2)如图2,在四边形ABCD中,∠B=∠C=90°,EF垂直平分AD,垂足为F,交BC于点E,已知AB=3,BC=8,CD=5.求证:直线EF为四边形ABCD的“等分积周线”;
(3)如图3,在△ABC中,AB=BC=6,AC=8,请你画出△ABC的一条“等分积周线”EF(要求:直线EF不过△ABC的顶点,交边AC于点F,交边BC于点E),并说明EF为“等分积周线”的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC、∠ACB的平分线交于点O,若∠A=40°,则∠BOC的度数为( )

A.40°B.80°C.100°D.110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,过B作BE⊥AD于E,过E作EF∥AC交AB于F,则下列结论:(1)AF=FE,(2)FE=FB,(3)FE=BE,(4)AF=BF,(5)BE =BF,成立的有( )

A.1 个B.2 个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在用描点法画二次函数
 的图象时,列出下面的表格:
的图象时,列出下面的表格:
…





…

…





…
根据表格提供的信息,下列说法错误的是( )
A. 该抛物线的对称轴是直线
 B. 该抛物线与
B. 该抛物线与 轴的交点坐标为
轴的交点坐标为C.
 D. 若点
D. 若点 是该抛物线上一点.则
是该抛物线上一点.则
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,垂足为E,若DE=2cm,则BD的长为_______.

相关试题

