Question

【题目】已知一次函数y=ax+b的图象上有两点A、B，它们的横坐标分别是3，－1，若二次函数y=x2的图象经过A、B两点．

（1）请求出一次函数的表达式；

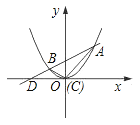
（2）设二次函数的顶点为C，求△ABC的面积．

Answer 1

【答案】（1）；（2）2．

【解析】

试题分析：（1）将A、B的横坐标代入抛物线的解析式中，即可求得A、B的坐标，然后将它们代入直线的解析式中，可得方程组，解方程组即可求得a、b的值，从而得一次函数的表达式；（2）抛物线y=x2的顶点是原点O，设直线AB与x轴的交点为D，先根据直线AB的解析式求出D点坐标，然后根据△ADO的面积减去△OBD的面积=△OAB的面积即可求得．

△OAB的面积．

试题解析：解：（1）设A点坐标为（3，m）；B点坐标为（-1，n）．

∵A、B两点在y=x2的图象上，∴m=×9=3，

n=×1=．

∴A（3，3），B（-1，）．

∵A、B两点又在y=ax+b的图象上，可得，

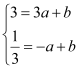，解得

∴一次函数的表达式是．

（2）如下图，设直线AB与x轴的交点为D，则D点坐标为（,0）,

S△ABC=S△ADC-S△BDC=××3-××1=2．