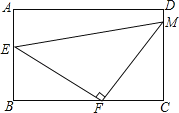
【题目】在矩形ABCD中,E、F、M分别为AB、BC、CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为 .

参考答案:
【答案】5![]() .
.
【解析】
试题分析:由四边形ABCD是矩形,得到∠B=∠C=90°,CD=AB=6,根据AE=3,DM=2,于是得到BE=3,CM=4,推出△BEF∽△CFM,得到关于BF的比例式,进而可求出EM,EF的长,再利用勾股定理即可求出EM的长.
解:∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD=AB=6,
∵AE=3,DM=2,
∴BE=3,CM=4,
∵EF⊥FM,
∴∠BEF+∠BFE=∠BFE+∠MFC=90°,
∴∠BEF=∠CFM,
∴△BEF∽△CFM,
∴![]() ,
,
∴![]() ,
,
解得:BF=3,或BF=4,
∴CF=4,或CF=3,
∴EF=![]() =5,FM=
=5,FM=![]() =5,
=5,
∴EM=![]() =5
=5![]() ,
,
故答案为:5![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列三角形中,可以构成直角三角形的有( )
A. 三边长分别为2,2,3 B. 三边长分别为3,3,5
C. 三边长分别为4,5,6 D. 三边长分别为1.5,2,2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】到△ABC三条边的距离相等的点是△ABC的( )
A. 三边中线的交点 B. 三条角平分线的交点
C. 三边上高的交点 D. 三边垂直平分线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:
①EG⊥FH;
②四边形EFGH是矩形;
③HF平分∠EHG;
④EG=
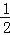 (BC﹣AD);
(BC﹣AD);⑤四边形EFGH是菱形.其中正确的个数是( )

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 两个关于某直线对称的图形是全等图形;
B. 两个图形全等,它们一定关于某直线对称;
C. 两个全等三角形对应点连线的垂直平分线就是它们的对称轴;
D. 两个三角形关于某直线对称,对称点一定在直线两旁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)填空:AB= ,BC= ;
(2)若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动.试探索:BC﹣AB的值是否随着时间的变化而改变?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.

(1)说明四边形ACEF是平行四边形;
(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.
相关试题

