【题目】如图1,把矩形![]() 放在平面直角坐标系中,边
放在平面直角坐标系中,边![]() 在
在![]() 轴上,边
轴上,边![]() 在
在![]() 轴上,连接
轴上,连接![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 平分
平分![]() 交
交![]() 于点
于点![]() .动点
.动点![]() 在线段
在线段![]() 上运动,过
上运动,过![]() 作
作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() .
.
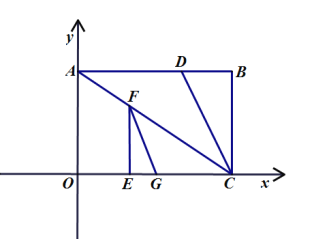
(1)当![]() 时,在线段
时,在线段![]() 上有一动点
上有一动点![]() ,
,![]() 轴上有一动点
轴上有一动点![]() ,连接
,连接![]() 当
当![]() 周长最小时,求
周长最小时,求![]() 周长的最小值及此时点
周长的最小值及此时点![]() 的坐标;
的坐标;
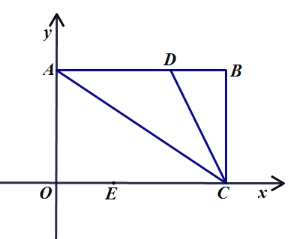
(2)如图2,在(1)问的条件下,点![]() 是直线
是直线![]() 上的一个动点,问:在
上的一个动点,问:在![]() 轴上是否存在
轴上是否存在![]() 点,使得
点,使得![]() 是以
是以![]() 为腰的等腰直角三角形?若存在,请直接写出
为腰的等腰直角三角形?若存在,请直接写出![]() 点及对应的
点及对应的![]() 点的坐标,若没有,请说明理由.
点的坐标,若没有,请说明理由.
参考答案:
【答案】(1)![]() 周长的最小值为6,N(0,1);(2)存在,P(
周长的最小值为6,N(0,1);(2)存在,P(![]() ,
,![]() ),对应Q(0,
),对应Q(0,![]() )或P(
)或P(![]() ,
,![]() ),对应Q(0,
),对应Q(0,![]() ).
).
【解析】
(1)根据角平分线、平行线以及矩形的性质得出∠EFG=30°,设EG=a,表达出△EFG的面积,求出a的值,进而求出OE的值,连接DE,DF,作点E关于y轴的对称点H,连接DH,证明△CEF≌△CDF(SAS),得到点E与点D关于AC对称,确定![]() 周长的最小值为DH,求出点D和点H的坐标,即可求出DH的值,待定系数法求出直线DH的解析式,即可求出点N的坐标;
周长的最小值为DH,求出点D和点H的坐标,即可求出DH的值,待定系数法求出直线DH的解析式,即可求出点N的坐标;
(2)待定系数法求出直线AC的解析式,设点P(p,![]() p+3),①若∠QPE=90°,PQ=PE,过点P作PK⊥y轴于点K,PJ⊥x轴于点J,证明△PKQ≌△PEJ(AAS),得到QK=EJ,PK=PJ,列出方程即可求出p,进而求出P和Q的坐标;②当∠QEP=90°时,EQ=EP,过点P作PR⊥x轴于点R,证明△OQE≌△REP(AAS),得到PR=OE=
p+3),①若∠QPE=90°,PQ=PE,过点P作PK⊥y轴于点K,PJ⊥x轴于点J,证明△PKQ≌△PEJ(AAS),得到QK=EJ,PK=PJ,列出方程即可求出p,进而求出P和Q的坐标;②当∠QEP=90°时,EQ=EP,过点P作PR⊥x轴于点R,证明△OQE≌△REP(AAS),得到PR=OE=![]() ,OQ=ER,列出方程即可求出p,进而得到P和Q的坐标即可.
,OQ=ER,列出方程即可求出p,进而得到P和Q的坐标即可.
解:(1)∵四边形OABC是矩形,
∴∠BCO=90°,BC=OA=3,
∵∠ACO=30°,
∴∠ACB=60°,
∵CD平分∠ACB,
则∠ACD=∠BCD=30°,
∵FG∥CD,
∴∠CFG=∠ACD=30°,
∴∠ACO=∠CFG=30°,
∴CG=FG,
∵EF⊥OC,∠ACO=30°,
∴∠EFC=60°,
∴∠EFG=60°-30°=30°,
设EG=a,则FG=2a,
∴EF=![]() ,
,
∴![]() ,即
,即![]() ,解得:a=
,解得:a=![]() ,
,
∴EF=![]() ,FG=CG=
,FG=CG=![]() ,
,
∴CE=CG+EG=![]() +
+![]() =2
=2![]() ,
,
∵OA=3,∠AOC=30°,
∴AC=6,OC=![]() ,
,
∴OE=![]() ,
,
连接DE,DF,作点E关于y轴的对称点H,连接DH,
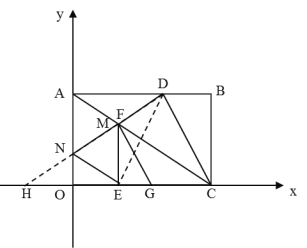
∵∠BCD=30°,BC=3,∠B=90°,
设BD=b,则DC=2b,
∴b2+32=(2b)2,解得:b=![]() ,则DC=2
,则DC=2![]() ,
,
∴CE=CD,
在△CEF与△CDF中,
CE=CD,∠ECF=∠DCF,CF=CF,
∴△CEF≌△CDF(SAS),
∴EF=DF,
∴CF垂直平分DE,
∴点E与点D关于AC对称,
∴![]() 周长的最小值为DH,
周长的最小值为DH,
∵BD=![]() ,AB=OC=3
,AB=OC=3![]() ,
,
∴AD=2![]() ,则D(2
,则D(2![]() ,3),
,3),
又∵点H(-![]() ,0),
,0),
∴DH=![]() ,
,
![]() 周长的最小值为6,
周长的最小值为6,
设直线DH的解析式为y=kx+t,
将D(2![]() ,3),H(-
,3),H(-![]() ,0)代入得:
,0)代入得: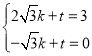 ,
,
解得:k=![]() ,t=1,
,t=1,
∴y=![]() x+1,
x+1,
当x=0时,y=1,
∴N(0,1)
(2)存在,
设直线AC为y=mx+n,将点A(0,3),C(3![]() ,0)代入得:
,0)代入得:
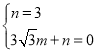 ,解得m=
,解得m=![]() ,n=3,
,n=3,
∴y=![]() x+3,
x+3,
设点P(p,![]() p+3),
p+3),
①若∠QPE=90°,PQ=PE,
如图①,过点P作PK⊥y轴于点K,PJ⊥x轴于点J,
∵∠KOJ=∠PKO=∠PJO=90°,
∴∠KPJ=90°,
∵∠QPK+∠KPE=∠JPE+∠KPE=90°,
∴∠QPK=∠EPJ,
又∵PQ=PE,∠PKQ=∠PJE=90°,
∴△PKQ≌△PEJ(AAS),
∴QK=EJ,PK=PJ,
即p=![]() p+3,解得:p=
p+3,解得:p=![]() ,
,
∴P(![]() ,
,![]() )
)
∴QK=EJ=![]() -
-![]() =
=![]() ,
,
∴OQ=OK+QK=![]() +
+![]() =
=![]() ,
,
∴Q(0,![]() );
);
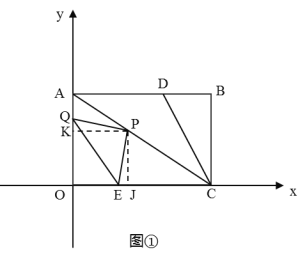
②当∠QEP=90°时,EQ=EP,
如图②,过点P作PR⊥x轴于点R,
∵∠QEP=90°,∠QOE=90°,
∴∠OQE+∠QEO=90°,∠QEO+∠PER=90°,
∴∠OQE=∠PER,
在△OQE与△REP中,
∠QOE=∠ERP=90°,∠OQE=∠PER,QE=EP,
∴△OQE≌△REP(AAS),
∴PR=OE=![]() ,OQ=ER,
,OQ=ER,
即![]() p+3=
p+3=![]() ,解得p=
,解得p=![]() ,
,
∴P(![]() ,
,![]() ),
),
∴OQ=ER=![]() -
-![]() =
=![]() ,
,
∴Q(0,![]() )
)
综上所述,P(![]() ,
,![]() ),对应Q(0,
),对应Q(0,![]() )或P(
)或P(![]() ,
,![]() ),对应Q(0,
),对应Q(0,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,A(-1,5)、B(-1,0),C(-4,3).

(1)△ABC的面积是 .
(2)在下图中画出△ABC向下平移2个单位,向右平移5个单位后的△A1B1C1.
(3)写出点A1、B1、C1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】清明节,除了扫墓踏青之外,传统时令小吃----青团也深受大家欢迎,知味观推出一款鲜花牛奶青团和一款芒果青团,鲜花牛奶青团每个售价是芒果青团的
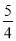 倍,4月份鲜花牛奶青团和芒果青团总计销售
倍,4月份鲜花牛奶青团和芒果青团总计销售 个,鲜花牛奶青团销售额为
个,鲜花牛奶青团销售额为 元,芒果青团销售额为
元,芒果青团销售额为 元.
元.(1)求鲜花牛奶青团和芒果青团的售价?
(2)5月份正值知味观店庆,决定再生产
 个青团回馈新老顾客,但考虑到芒果青团较受欢迎,同时也考虑受机器设备限制,因此芒果青团的个数不少于鲜花牛奶青团个数的
个青团回馈新老顾客,但考虑到芒果青团较受欢迎,同时也考虑受机器设备限制,因此芒果青团的个数不少于鲜花牛奶青团个数的 ,不多于鲜花牛奶青团的
,不多于鲜花牛奶青团的 倍,其中,鲜花牛奶青团每个让利
倍,其中,鲜花牛奶青团每个让利 元销售,芒果青团售价不变,并且让利后的鲜花牛奶青团售价不得低于芒果青团售价的
元销售,芒果青团售价不变,并且让利后的鲜花牛奶青团售价不得低于芒果青团售价的 ,问:知味观如何设计生产方案?使总销售额最大.
,问:知味观如何设计生产方案?使总销售额最大. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
 .
.请结合题意,完成本题的解答.
(1)解不等式①,得 ,依据是: .
(2)解不等式③,得 .
(3)把不等式①,②和③的解集在数轴上表示出来.

(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
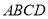 中,
中, ,
,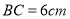 ,点
,点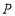 沿
沿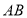 边从点
边从点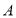 开始向点
开始向点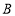 以
以 秒的速度移动;点
秒的速度移动;点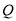 沿
沿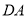 边从点
边从点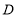 开始向点
开始向点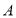 以
以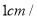 秒的速度移动,如果
秒的速度移动,如果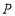 、
、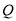 同时出发,用
同时出发,用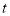 (秒)表示移动的时间(
(秒)表示移动的时间(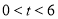 ).
).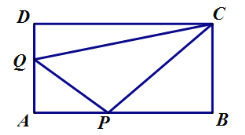
(1)当
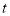 为何值时,
为何值时,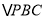 为等腰直角三角形.
为等腰直角三角形.(2)求当移动到
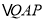 为等腰直角三角形时斜边
为等腰直角三角形时斜边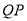 的长.
的长. -
科目: 来源: 题型:
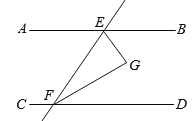
查看答案和解析>>【题目】如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,
(1)若∠AEF=50°,求∠EFG的度数.
(2)判断EG与FG的位置关系,并说明理由.
相关试题

