【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 秒的速度移动;点
秒的速度移动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 秒的速度移动,如果
秒的速度移动,如果![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间(
(秒)表示移动的时间(![]() ).
).
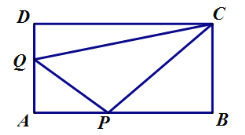
(1)当![]() 为何值时,
为何值时,![]() 为等腰直角三角形.
为等腰直角三角形.
(2)求当移动到![]() 为等腰直角三角形时斜边
为等腰直角三角形时斜边![]() 的长.
的长.
参考答案:
【答案】(1)当![]() ,
,![]() 为等腰直角三角形;(2)
为等腰直角三角形;(2)![]()
【解析】
(1)由矩形的性质得出![]() ,
,![]() ,当
,当![]() 时,
时,![]() 为等腰直角三角形,得出方程,解方程即可;
为等腰直角三角形,得出方程,解方程即可;
(2)由题意得出![]() ,
,![]() ,
,![]() 当
当![]() 时,
时,![]() 为等腰直角三角形.得出方程,解方程求出
为等腰直角三角形.得出方程,解方程求出![]() ,得出
,得出![]() 、
、![]() 的长度,再由勾股定理求出
的长度,再由勾股定理求出![]() 即可.
即可.
(1)解:对于任何时刻![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,
当![]() 时,
时,![]() 为等腰直角三角形,
为等腰直角三角形,
即![]() ,
,
解得:![]()
![]() 当
当![]() ,
,![]() 为等腰直角三角形
为等腰直角三角形
(2)解:![]() ,
,![]() ,
,![]()
当![]() 时,
时,![]() 为等腰直角三角形.
为等腰直角三角形.
即![]() .
.
解得:![]() (秒).
(秒).
![]() 当
当![]() 秒时,
秒时,![]() 为等腰直角三角形.
为等腰直角三角形.
此时![]() ,
,![]() ,
,
在![]() 中,
中,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】清明节,除了扫墓踏青之外,传统时令小吃----青团也深受大家欢迎,知味观推出一款鲜花牛奶青团和一款芒果青团,鲜花牛奶青团每个售价是芒果青团的
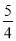 倍,4月份鲜花牛奶青团和芒果青团总计销售
倍,4月份鲜花牛奶青团和芒果青团总计销售 个,鲜花牛奶青团销售额为
个,鲜花牛奶青团销售额为 元,芒果青团销售额为
元,芒果青团销售额为 元.
元.(1)求鲜花牛奶青团和芒果青团的售价?
(2)5月份正值知味观店庆,决定再生产
 个青团回馈新老顾客,但考虑到芒果青团较受欢迎,同时也考虑受机器设备限制,因此芒果青团的个数不少于鲜花牛奶青团个数的
个青团回馈新老顾客,但考虑到芒果青团较受欢迎,同时也考虑受机器设备限制,因此芒果青团的个数不少于鲜花牛奶青团个数的 ,不多于鲜花牛奶青团的
,不多于鲜花牛奶青团的 倍,其中,鲜花牛奶青团每个让利
倍,其中,鲜花牛奶青团每个让利 元销售,芒果青团售价不变,并且让利后的鲜花牛奶青团售价不得低于芒果青团售价的
元销售,芒果青团售价不变,并且让利后的鲜花牛奶青团售价不得低于芒果青团售价的 ,问:知味观如何设计生产方案?使总销售额最大.
,问:知味观如何设计生产方案?使总销售额最大. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把矩形
 放在平面直角坐标系中,边
放在平面直角坐标系中,边 在
在 轴上,边
轴上,边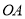 在
在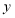 轴上,连接
轴上,连接 ,且
,且 ,过点
,过点 作
作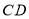 平分
平分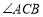 交
交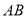 于点
于点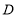 .动点
.动点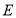 在线段
在线段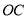 上运动,过
上运动,过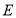 作
作 交
交 于
于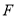 ,过
,过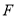 作
作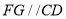 交
交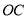 于
于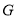 .
.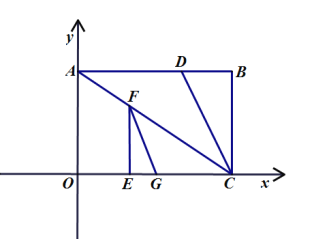
(1)当
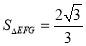 时,在线段
时,在线段 上有一动点
上有一动点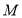 ,
,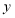 轴上有一动点
轴上有一动点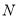 ,连接
,连接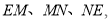 当
当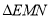 周长最小时,求
周长最小时,求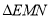 周长的最小值及此时点
周长的最小值及此时点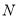 的坐标;
的坐标;(2)如图2,在(1)问的条件下,点
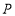 是直线
是直线 上的一个动点,问:在
上的一个动点,问:在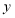 轴上是否存在
轴上是否存在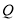 点,使得
点,使得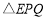 是以
是以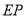 为腰的等腰直角三角形?若存在,请直接写出
为腰的等腰直角三角形?若存在,请直接写出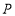 点及对应的
点及对应的 点的坐标,若没有,请说明理由.
点的坐标,若没有,请说明理由.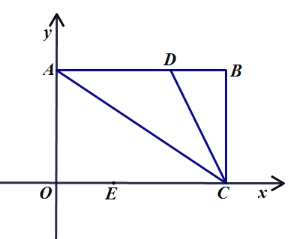
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
 .
.请结合题意,完成本题的解答.
(1)解不等式①,得 ,依据是: .
(2)解不等式③,得 .
(3)把不等式①,②和③的解集在数轴上表示出来.

(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,
(1)若∠AEF=50°,求∠EFG的度数.
(2)判断EG与FG的位置关系,并说明理由.
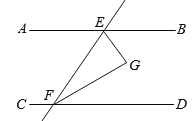
-
科目: 来源: 题型:
查看答案和解析>>【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售件,每件盈利元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
相关试题

