【题目】探究;
(![]() )如图,
)如图, ![]() 、
、![]() 为
为![]() 的边
的边![]() 、
、![]() 上的两定点,在
上的两定点,在![]() 上求作一点
上求作一点![]() ,使
,使![]() 的周长最短.(不写作法)
的周长最短.(不写作法)

(![]() )如图,矩形
)如图,矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,点
的中点,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的动点,求四边形
上的动点,求四边形![]() 周长的最小值.
周长的最小值.

(![]() )如图,正方形
)如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 为
为![]() 边中点,在边
边中点,在边![]() 、
、![]() 、
、![]() 上分别确定点
上分别确定点![]() 、
、![]() 、
、![]() .使得四边形
.使得四边形![]() 周长最小,并求出最小值.
周长最小,并求出最小值.

参考答案:
【答案】(1)作图见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)
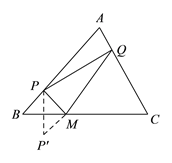
试题分析:(1)利用轴对称图形的性质,作点P关于BC的对称点P′,连接P′Q,交BC于点M,则M是所求的点;(2)如图,延长EB至E'使E' B=EB,延长FD至F'使F' D=FD,连接E' F'交BC、CD于M、N.此时四边形EFNM周长最小.根据勾股定理求得EF、E' F'的长,即可得四边形OMNP周长的最小值;(3)如图,延长![]() 到
到![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() .作
.作![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .连
.连![]() 交
交![]() 于
于![]() ,即为周长最小.根据正方形的性质和轴对称的性质易得
,即为周长最小.根据正方形的性质和轴对称的性质易得![]() 、
、![]() 、
、![]() 为各边中点,所以四边形
为各边中点,所以四边形![]() 周长的最小值为
周长的最小值为![]() .
.
试题解析:
(![]() )如图,作点
)如图,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是所求的点.
是所求的点.
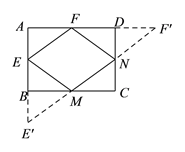
(![]() )如图,延长
)如图,延长![]() 至
至![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .此时四边形
.此时四边形![]() 周长最小.
周长最小.
周长![]()
![]()
![]() .
.
(![]() )如图,延长
)如图,延长![]() 到
到![]() 使
使![]() ,延长
,延长![]() 至
至![]() 使
使![]() .
.
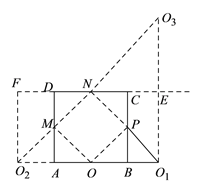
作![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .
.
连![]() 交
交![]() 于
于![]() ,即为周长最小.
,即为周长最小.
易得![]() 、
、![]() 、
、![]() 为各边中点,周长为
为各边中点,周长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有红、黄、蓝三种颜色的球(除颜色外其余都相同),
其中红球有1个,蓝球有1个,现从中任意摸出一个是红球的概率为
 .
. (1)求袋中黄球的个数.
(2)第一次摸出一个球(放回),第二次再摸一个球,请用画树状图或列表法求两次摸到都是红球的概率.
(3)若规定每次摸到红球得5分,每次摸到黄球得3分,每次摸到蓝球得1分,小芳摸6次球(每次摸1个球,摸后放回)合计得20分,请直接写出小芳有哪几种摸法?(不分球颜色的先后顺序)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式不能用平方差公式计算的是( )
A.(a+b)(a-b)B.(-a+b)(-a-b)C.(-a+b)(a-b)D.(a+b)( -a + b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
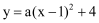 与x轴交于点A,B,与
与x轴交于点A,B,与 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】合并同类项:2ab+3a﹣4ab+5a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD=AE ,添加下列条件仍无法证明△ABE≌△ACD的是( )

A. AB=AC B. BE=CD C. ∠B=∠C D. ∠ADC=∠AEB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

相关试题

