【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

参考答案:
【答案】(1)C(1,-4).(2)证明见解析;(3)∠APB=135°,P(1,0).
【解析】试题分析:(1)过C作CD⊥Y轴于D,证出△ABO≌△BCD,再由OB=DC,OA=DB得出C(1,-4);
(2)证出△APB≌△CQB,进而得出PA=CQ;
(3)由C、P、Q三点共线,得∠CQB=135°,即∠APB=135°,进而∠OPB=45°,得P(1,0).
试题解析:(1)过C作CD⊥Y轴于D,
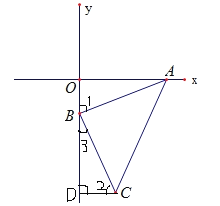
∴∠AOB=∠BDC=90°, ∠2+∠3=90°,
∵BC⊥AB,
∴∠1+∠3=90°,
∴∠1=∠2,
在△ABO和△BCD中, 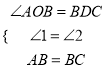 ,
,
∴△ABO≌△BCD,
∴OB=DC, OA=DB
∴C(1,-4);
(2)∵∠ABQ+∠QBC=∠PBA+∠ABQ=90°,
∴∠QBC=∠PBA,
在△APB和△CQB中, 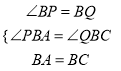 ,
,
∴△APB≌△CQB,(AAS)
∴AP=CQ;
(2)∵△APB≌△CQB,
∴∠APB=∠CQB,
∵由C、P、Q三点共线,
∴∠CQB=135°,即∠APB=135°,
∴∠OPB=45°,
∴P(1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究;
(
 )如图,
)如图,  、
、 为
为 的边
的边 、
、 上的两定点,在
上的两定点,在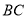 上求作一点
上求作一点 ,使
,使 的周长最短.(不写作法)
的周长最短.(不写作法)
(
 )如图,矩形
)如图,矩形 中,
中,  ,
,  ,
,  、
、 分别为边
分别为边 、
、 的中点,点
的中点,点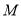 、
、 分别为
分别为 、
、 上的动点,求四边形
上的动点,求四边形 周长的最小值.
周长的最小值.
(
 )如图,正方形
)如图,正方形 的边长为
的边长为 ,点
,点 为
为 边中点,在边
边中点,在边 、
、 、
、 上分别确定点
上分别确定点 、
、 、
、 .使得四边形
.使得四边形 周长最小,并求出最小值.
周长最小,并求出最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】合并同类项:2ab+3a﹣4ab+5a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD=AE ,添加下列条件仍无法证明△ABE≌△ACD的是( )

A. AB=AC B. BE=CD C. ∠B=∠C D. ∠ADC=∠AEB
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列四种说法中,①ab是一次单项式;②单项式﹣x2y的系数是﹣1;③1+x2﹣4x是按x的降幂排列的;④数字3是单项式.不正确的是( )
A.①③
B.②③
C.②④
D.①② -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小颖做掷骰子的游戏,规则如下:
① 游戏前,每人选一个数字;
② 每次同时掷两枚均匀骰子;
③ 如果同时掷得的两枚骰子点数之和,与谁所选数字相同,那么谁就获胜.
(1)在下表中列出同时掷两枚均匀骰子所有可能出现的结果:
第2枚骰子掷得
第1枚 的点数
骰子掷得的点数
1
2
3
4
5
6
1
2
3
4
5
6
(2)小明选的数字是5,小颖选的数字是6.如果你也加入游戏,你会选什么数字,使自
己获胜的概率比他们大?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )

A. a2﹣b2=(a﹣b)2 B. (a+b)2=a2+2ab+b2
C. (a﹣b)2=a2﹣2ab+b2 D. a2﹣b2=(a+b)(a﹣b)
相关试题

