搜索
【题目】如图，在平面直角坐标系中，矩形OABC的顶点A在y轴上，C在x轴上，把矩形OABC沿对角线AC所在的直线翻折，点B恰好落在反比例函数
的图象上的点
处，
与y轴交于点D，已知
，
．
求
的度数；
求反比例函数的函数表达式；
若Q是反比例函数图象上的一点，在坐标轴上是否存在点P，使以P，Q，C，D为顶点的四边形是平行四边形？若存在，请求出P点的坐标；若不存在，请说明理由．
参考答案：
【答案】（1）
．（2）
．（3）满足条件的点P坐标为
，
，
，
，
．
【解析】
（1）
;
（2）求出B’的坐标即可；
（3）分五种情况，分别画出图形可解决问题.
解：
四边形ABCO是矩形，
，
，
．
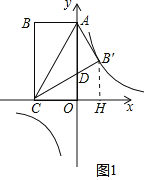
如图1中，作
轴于H．
，
，
，
，
，
，
，
，
反比例函数
的图象经过点
，
，
．
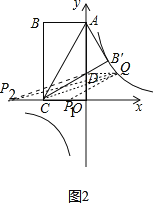
如图2中，作
轴交于
，以DQ为边构造平行四边形可得，；
如图3中，作
交于
，以
为边构造平行四边形可得，；
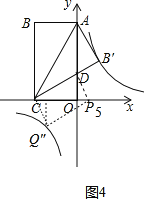
如图4中，当
，以
为边构造平行四边形可得，
综上所述，满足条件的点P坐标为，，，，．
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的解题过程，并在括号内填上依据.如图，EF∥AD,∠1=∠2,∠BAC=85°.求∠AGD的度数
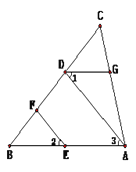
解： ∵EF∥AD,
∴∠2=____( )
又∵∠1=∠2
∴∠1=∠3
∴ ∥____( )
∴∠BAC+____=180°
∵∠BAC=85°
∴∠AGD=950
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠B=90°，BC=5
，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF． 
（1）求证：AE=DF；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．
（3）当t为何值时，△DEF为直角三角形？请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】定义：我们把对角线相等的四边形叫做和美四边形．
请举出一种你所学过的特殊四边形中是和美四边形的例子．
如图1，E，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点，已知四边形EFGH是菱形，求证：四边形ABCD是和美四边形；
如图2，四边形ABCD是和美四边形，对角线AC，BD相交于O，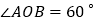
，E、F分别是AD、BC的中点，请探索EF与AC之间的数量关系，并证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
小明想探究函数
的性质，他借助计算器求出了y与x的几组对应值，并在平面直角坐标系中画出了函数图象：x
…
-3
-2
-1
1
2
3
…
y
…
2.83
1.73
0
0
1.73
2.83
…
小聪看了一眼就说：“你画的图象肯定是错误的．”
请回答：小聪判断的理由是_____________．请写出函数
的一条性质：_____________． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线
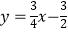与抛物线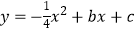 
交于A、B两点，点A在x轴上，点B的横坐标为﹣8．
（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E．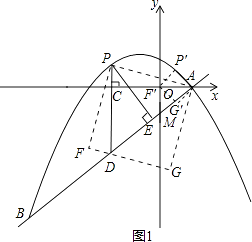
①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的最大值；
②连接PA，以PA为边作图示一侧的正方形APFG．随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】某校七年级（1）班共46人，前段时间有一位同学身患重病，其余同学献“爱心”为其捐款，共捐得156元，捐款情况见下表，由于记录的同学不小心，造成捐款3元和4元的人数看不清楚了.请你根据表格提供的信息，求出捐款3元和4元的人数分别是多少？
相关试题
