【题目】如图,在平面直角坐标系中,直线 ![]() 与抛物线
与抛物线 ![]() 交于A、B两点,点A在x轴上,点B的横坐标为﹣8.
交于A、B两点,点A在x轴上,点B的横坐标为﹣8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.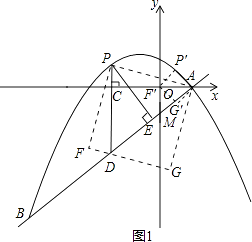
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
参考答案:
【答案】
(1)
解:对于 ![]() ,当y=0,x=2.当x=﹣8时,y=﹣
,当y=0,x=2.当x=﹣8时,y=﹣ ![]() .
.
∴A点坐标为(2,0),B点坐标为 ![]() .
.
由抛物线 ![]() 经过A、B两点,
经过A、B两点,
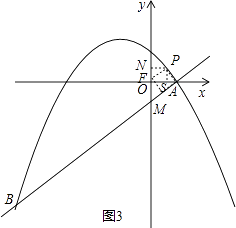
得 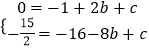
解得 ![]() .
.
∴ ![]() .
.
(2)
解:①设直线 ![]() 与y轴交于点M,
与y轴交于点M,
当x=0时,y= ![]() .∴OM=
.∴OM= ![]() .
.
∵点A的坐标为(2,0),∴OA=2.∴AM= ![]() .
.
∵OM:OA:AM=3:4:5.
由题意得,∠PDE=∠OMA,∠AOM=∠PED=90°,∴△AOM∽△PED.
∴DE:PE:PD=3:4:5.
∵点P是直线AB上方的抛物线上一动点,
∵PD⊥x轴,
∴PD两点横坐标相同,
∴PD=yP﹣yD=﹣ ![]() ﹣
﹣ ![]() ﹣(
﹣( ![]() x﹣
x﹣ ![]() )
)
=﹣ ![]() x2﹣
x2﹣ ![]() x+4,
x+4,
∴ ![]()
= ![]() .
.
∴ ![]() .
.
∴x=﹣3时,l最大=15.
②当点G落在y轴上时,如图2,由△ACP≌△GOA得PC=AO=2,
即 ![]() ,解得
,解得 ![]() ,
,
所以 ![]() ,
,
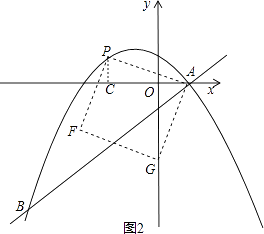
如图3,过点P作PN⊥y轴于点N,过点P作PS⊥x轴于点S,
由△PNF≌△PSA,
PN=PS,可得P点横纵坐标相等,
故得当点F落在y轴上时,
x=﹣ ![]() ﹣
﹣ ![]() x+
x+ ![]() ,解得x=
,解得x= ![]() ,
,
可得 ![]() ,
, ![]() (舍去).
(舍去).
综上所述:满足题意的点P有三个,分别是 ![]()
![]() .
.
【解析】(1)利用待定系数法求出b,c即可;(2)①根据△AOM∽△PED,得出DE:PE:PD=3:4:5,再求出PD=yP﹣yD求出二函数最值即可;②当点G落在y轴上时,由△ACP≌△GOA得PC=AO=2,即 ![]() ,解得
,解得 ![]() ,所以得出P点坐标,当点F落在y轴上时,x=
,所以得出P点坐标,当点F落在y轴上时,x= ![]() ,解得x=
,解得x= ![]() ,可得P点坐标.
,可得P点坐标.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把对角线相等的四边形叫做和美四边形.
 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子. 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形; 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,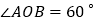 ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在y轴上,C在x轴上,把矩形OABC沿对角线AC所在的直线翻折,点B恰好落在反比例函数
 的图象上的点
的图象上的点 处,
处, 与y轴交于点D,已知
与y轴交于点D,已知 ,
, .
. 求
求 的度数;
的度数; 求反比例函数
求反比例函数 的函数表达式;
的函数表达式; 若Q是反比例函数
若Q是反比例函数 图象上的一点,在坐标轴上是否存在点P,使以P,Q,C,D为顶点的四边形是平行四边形?若存在,请求出P点的坐标;若不存在,请说明理由.
图象上的一点,在坐标轴上是否存在点P,使以P,Q,C,D为顶点的四边形是平行四边形?若存在,请求出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明想探究函数
 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:x
…
-3
-2
-1
1
2
3
…
y
…
2.83
1.73
0
0
1.73
2.83
…

小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是_____________.请写出函数
 的一条性质:_____________.
的一条性质:_____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级(1)班共46人,前段时间有一位同学身患重病,其余同学献“爱心”为其捐款,共捐得156元,捐款情况见下表,由于记录的同学不小心,造成捐款3元和4元的人数看不清楚了.请你根据表格提供的信息,求出捐款3元和4元的人数分别是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣1,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组
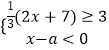 无解,且使关于x的分式方程
无解,且使关于x的分式方程  =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
A.﹣2
B.﹣3
C.-
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
 的表达式为
的表达式为 ,点A,B的坐标分别为
,点A,B的坐标分别为(1,0),(0,2),直线AB与直线
 相交于点P.
相交于点P.(1)求直线AB的表达式;
(2)求点P的坐标;
(3)若直线
 上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
相关试题

