【题目】如图,反比例函数 y=![]() 的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
(1)求反比例函数与一次函数的函数关系式;
(2)根据图象,回答当一次函数的值大于反比例函数的值时,x 的取值范围为________;
(3) 连接AO、BO,则△ABO的面积是_________;

参考答案:
【答案】 x<﹣3或0<x<1 4
【解析】试题分析:(1)把点![]() 代入反比例函数
代入反比例函数![]() 即可求出
即可求出![]() 的值,进而求出反比例函数的解析式;再把点B的坐标代入反比例函数的关系式求出
的值,进而求出反比例函数的解析式;再把点B的坐标代入反比例函数的关系式求出![]() 的值,把
的值,把![]() 两点坐标代入一次函数的关系式即可求出一次函数的关系式;
两点坐标代入一次函数的关系式即可求出一次函数的关系式;
(2)由(1)中![]() 两点的坐标,结合函数图象可直接得出结论;
两点的坐标,结合函数图象可直接得出结论;
(3)根据(1)中求出的一次函数的关系式求出点![]() 的坐标,再根据
的坐标,再根据![]() 进行解答;
进行解答;
试题解析:(1)∵![]() 在
在![]() 的图象上,
的图象上,
![]()
![]()
又∵![]() 在
在![]() 的图象上,
的图象上,
![]() 即
即![]()
∴![]() ,
,
解得: ![]()
∴反比例函数的解析式为![]() ,一次函数的解析式为
,一次函数的解析式为![]()
(2)从图象上可知,当![]() 或
或![]() 时,反比例函数的值大于一次函数的值.
时,反比例函数的值大于一次函数的值.
故答案为: ![]() 或
或![]() .
.
(3)设一次函数与![]() 轴交点为
轴交点为![]() ,
,
令一次函数值![]() ,得
,得![]()
![]()
![]()
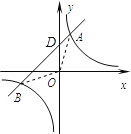
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
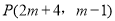 ,试分别根据下列条件,求点
,试分别根据下列条件,求点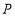 的坐标.
的坐标.(1)点
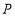 在
在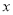 轴上;
轴上;(2)点
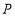 在过点
在过点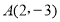 且与
且与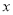 轴平行的直线上;
轴平行的直线上;(3)点
 到两坐标轴的距离相等.
到两坐标轴的距离相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
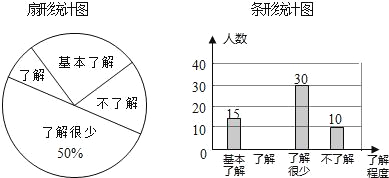
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠3=∠B,求证:EF∥BC,请你补充完成下面的推导过程.
证明:∵∠1+∠2=180°(已知)
∠2=∠4( )
∴∠ +∠4=180°(等量代换)
∴DF∥AB( )
∴∠B=∠FDH( )
∵∠3=∠B( )
∴∠3=∠ ( )
∴EF∥BC( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OE平分∠BOD,∠AOC=70°,∠DOF=90°.

(1)图中与∠EOF互余的角是 ;
(2)求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠ACB=∠DFE=90°,∠A=∠FDE=60°,AC=1. 固定△ABC不动,将△DEF进行如下操作:
(1) 如图 (1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.
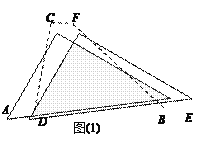
(2)如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.

(3)如图(3),△DEF的F点固定在AB的中点,然后绕F点按顺时针方向旋转△DEF,使EF交在AC边上于M,FD交BC于N,若FM=x,FN=y,试求y关于x的函数关系式。

相关试题

