【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
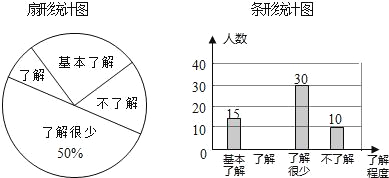
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
参考答案:
【答案】(1) 60,90;(2)见解析;(3) 300人
【解析】
(1)由了解很少的有30人,占50%,可求得接受问卷调查的学生数,继而求得扇形统计图中“基本了解”部分所对应扇形的圆心角;
(2)由(1)可求得了解的人数,继而补全条形统计图;
(3)利用样本估计总体的方法,即可求得答案.
解:(1)∵了解很少的有30人,占50%,
∴接受问卷调查的学生共有:30÷50%=60(人);
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为:![]() ×360°=90°;
×360°=90°;
故答案为:60,90;
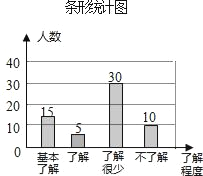
(2)60﹣15﹣30﹣10=5;
补全条形统计图得:
(3)根据题意得:900×![]() =300(人),
=300(人),
则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人.
-
科目: 来源: 题型:
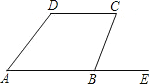
查看答案和解析>>【题目】如图,BE是AB的延长线,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2011年国家对“酒后驾车”加大了处罚力度,出台了不准酒后驾车的禁令.某记者在一停车场对开车的司机进行了相关的调查,本次调查结果有四种情况:①偶尔喝点酒后开车;②已戒酒或从来不喝酒;③喝酒后不开车或请专业司机代驾;④平时喝酒,但开车当天不喝酒.将这次调查悄况整理并绘制了如下尚不完整的统计图,请根据相关信息,解答下列问题
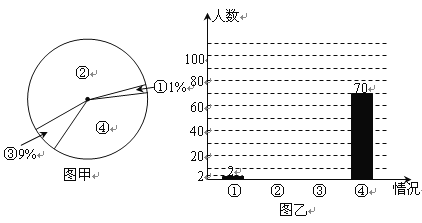
(1)该记者本次一共调查了 名司机.
(2)求图甲中④所在扇形的圆心角,并补全图乙.
(3)在本次调查中,记者随机采访其中的一名司机,求他属第②种情况的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
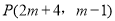 ,试分别根据下列条件,求点
,试分别根据下列条件,求点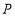 的坐标.
的坐标.(1)点
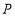 在
在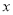 轴上;
轴上;(2)点
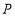 在过点
在过点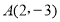 且与
且与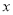 轴平行的直线上;
轴平行的直线上;(3)点
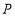 到两坐标轴的距离相等.
到两坐标轴的距离相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠3=∠B,求证:EF∥BC,请你补充完成下面的推导过程.
证明:∵∠1+∠2=180°(已知)
∠2=∠4( )
∴∠ +∠4=180°(等量代换)
∴DF∥AB( )
∴∠B=∠FDH( )
∵∠3=∠B( )
∴∠3=∠ ( )
∴EF∥BC( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数 y=
 的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).(1)求反比例函数与一次函数的函数关系式;
(2)根据图象,回答当一次函数的值大于反比例函数的值时,x 的取值范围为________;
(3) 连接AO、BO,则△ABO的面积是_________;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.

相关试题

