【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60 米的斜坡AB进行改造,在斜坡中点D 处挖去部分坡体(阴影表示),修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE.

(1)若修建的斜坡BE 的坡角为36°,则平台DE的长约为多少米?
(2)在距离坡角A点27米远的G处是商场主楼,小明在D点测得主楼顶部H 的仰角为30°,那么主楼GH高约为多少米?
(结果取整数,参考数据:sin 36°=0.6,cos 36°=0.8,tan 36°=0.7,![]() =1.7)
=1.7)
参考答案:
【答案】(1)4米;(2)45米.
【解析】试题分析:(1)根据题意得出,∠BEF=36°,进而得出EF的长,即可得出答案;(2)利用在Rt△DPA中,DP=![]() AD,以及PA=ADcos30°进而得出DM的长,利用HM=DMtan30°得出即可.
AD,以及PA=ADcos30°进而得出DM的长,利用HM=DMtan30°得出即可.
试题解析:(1)∵修建的斜坡BE的坡角(即∠BEF)为36°,∴∠BEF=36°,∵∠DAC=∠BDF=30°,AD=BD=30,∴BF=![]() BD=15,DF=15
BD=15,DF=15![]() ,EF=
,EF=![]() =
=![]() ,故DE=DF-EF=15
,故DE=DF-EF=15![]() -
-![]() ≈4(米);
≈4(米);

(2)过点D作DP⊥AC,垂足为P.在Rt△DPA中,DP=![]() AD=
AD=![]() ×30=15,PA=ADcos30°=
×30=15,PA=ADcos30°=![]() ×30=15
×30=15![]() ,在矩形DPGM中,MG=DP=15,DM=PG=15
,在矩形DPGM中,MG=DP=15,DM=PG=15![]() +27,在Rt△DMH中,HM=DMtan30°=
+27,在Rt△DMH中,HM=DMtan30°=![]() ×(15
×(15![]() +27)=15+9
+27)=15+9![]() ,GH=HM+MG=15+15+9
,GH=HM+MG=15+15+9![]() ≈45米.答:建筑物GH高约为45米.
≈45米.答:建筑物GH高约为45米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x<-2,则下列不等式成立的是( )
A. x2>-2x B. x2≥-2x C. x2<-2x D. x2≤-2x
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,若EG平分∠BEF,FM平分∠EFD交EG于M,EN平分∠AEF,则与∠FEM互余的角有( )
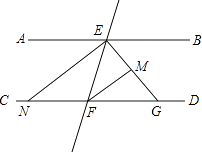
A.3个
B.4个
C.5个
D.6个 -
科目: 来源: 题型:
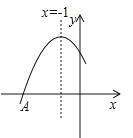
查看答案和解析>>【题目】如图是二次函数
 图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:
图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:①abc<0,②
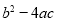 >0,③4b+c<0,④若B(
>0,③4b+c<0,④若B( ,
,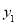 )、C(
)、C(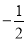 ,
, )为函数图象上的两点,则
)为函数图象上的两点,则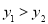 ,⑤当﹣3≤x≤1时,y≥0.
,⑤当﹣3≤x≤1时,y≥0.其中正确的结论是(填写代表正确结论的序号) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“三角形中至少有一个内角不大于60°”,首先应假设这个三角形中( )
A. 没有一个角不小于60°B. 没有一个角不大于60°
C. 所有内角不大于60°D. 所有内角不小于60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④两个半圆是等弧。其中正确的有 ( )
A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为5㎝,P到圆心O的距离为6㎝,则点P在⊙O( )
A. 外部B. 内部C. 圆上D. 不能确定
相关试题

