【题目】某商场计划采购甲、乙、丙三种型号的“格力”牌空调共25台.三种型号的空调进价和售价如下表:
种类价格 | 甲 | 乙 | 丙 |
进价(元/台) | 1600 | 1800 | 2400 |
售价(元/台) | 1800 | 2050 | 2600 |
商场计划投入总资金5万元,所购进的甲、丙型号空调数量相同,乙型号数量不超过甲型号数量的一半.若设购买甲型号空调x台,所有型号空调全部售出后获得的总利润为W元.
(1)求W与x之间的函数关系式.
(2)商场如何采购空调才能获得最大利润?
(3)由于原材料上涨,商场决定将丙型号空调的售价提高a元(a≥100),其余型号售价不变,则商场又该如何采购才能获得最大利润?
参考答案:
【答案】(1)![]() =
=![]() ,(2)购进甲10台,乙5台,丙10台时利润最大
,(2)购进甲10台,乙5台,丙10台时利润最大
(3)即购进甲12台,乙1台,丙12台.
【解析】解:(1)由题意知:丙型号为![]() 台,乙型号为
台,乙型号为![]() 台,则
台,则
![]()
=![]() ………………………………………………………………2分
………………………………………………………………2分
(2)依题意得: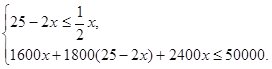 ……………………………3分
……………………………3分
解得![]() ………………………………………………………………4分
………………………………………………………………4分
又![]() 为正整数
为正整数
![]() 取10,11,12 ………………………………………………………………5分
取10,11,12 ………………………………………………………………5分
![]() 随
随![]() 增大而减小
增大而减小
![]() 当
当![]() 时,
时, ![]() 最大.
最大.
即购进甲10台,乙5台,丙10台时利润最大.……………………………………6分
(3)依题意得: ![]()
![]() ………………………………………………8分
………………………………………………8分
![]() 当
当![]() 时,
时, ![]() ,所以有三种方案:
,所以有三种方案:
即购进甲、丙两种型号各10台,乙5台
或购进甲、丙两种型号各11台,乙3台
或购进甲、丙两种型号各12台,乙1台
![]() 当
当![]() 时,
时, ![]() ,所以当
,所以当![]() 取12时,
取12时, ![]() 最大.
最大.
即购进甲12台,乙1台,丙12台.………………………………………10分
(1)总利润=甲型号空调利润+乙型号空调利润+丙型号空调利润,根据此关系计算即可;
(2)据题意列表达式组求解;
用含x的代数式表示利润W,根据x的取值范围和一次函数的性质求解
(3)根据(1)中的等量关系可得出一个关于总利润和a的函数关系式,根据函数性质和a的取值范围,判断出不同情况下哪种利润最大.
-
科目: 来源: 题型:
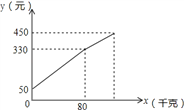
查看答案和解析>>【题目】李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)李大爷自带的零钱是 元;
(2)降价前他每千克蜜橘出售的价格是 元/千克;
(3)卖了几天,南丰蜜橘卖相不好了,随后他按每千克下降1.5元将剩下的蜜橘售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的蜜橘?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
(4)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
-
科目: 来源: 题型:
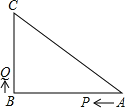
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其 中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)当t=2秒时,求PQ的长;
(2)求出发时间为几秒时,△PQB是等腰三角形?
(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.(直接写答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=2,ab=﹣1,则(a-b)2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形、矩形、正方形都具有的性质是( )
A. 对角线相等且互相平分 B. 对角线相等且互相垂直平分
C. 对角线互相平分 D. 四条边相等,四个角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两条边长分别为3和7,那么它的周长等于 .
相关试题

