搜索
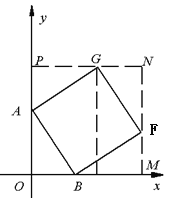
【题目】如图，在平面直角坐标系中，点B，C的坐标分别为（2，0）和（6，0）．
（1）确定A、D、E、F、G的坐标；
（2）求四边形ABFG的面积．
参考答案：
【答案】（1）A（0，3），D（8，1），E（7，3），F（5，2），G（3，5）；（2）13
【解析】
（1）观察图象，根据已知条件即可确定A、D、E、F、G的坐标；（2）如图分别过G，F作直线垂直于y轴和x轴，垂足分别为P，M，两条直线交于点N．利用“割补法”求四边形ABFG的面积即可．
（1）A（0，3），D（8，1），E（7，3），F（5，2），G（3，5）．
（2）如图，分别过G，F作直线垂直于y轴和x轴，垂足分别为P，M，两条直线交于点N．则P（0，5），M（5，0），N（5，5），
正方形OMNP面积为5×5＝25；S△AOB＝
×2×3＝3，S△BMF＝×3×2＝3，S△APG＝×2×3＝3，S△GFN＝×2×3＝3，故S△BFG＝25－3－3－3－3＝13．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某文化用品商店用2000元购进一批学生书包，面市后发现供不应求，商店又购进第二批同样的书包，所购数量是第一批购进数量的3倍，但单价贵了4元，结果第二批用了6300元．
（1）求第一批购进书包的单价是多少元？
（2）若商店销售这两批书包时，每个售价都是120元，全部售出后，商店共盈利多少元？ -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知A，B是抛物线y=ax2（a＞0）上两个不同的点，其中A在第二象限，B在第一象限．
（1）如图1所示，当直线AB与x轴平行，∠AOB=90°，且AB=2时，求此抛物线的解析式和A，B两点的横坐标的乘积；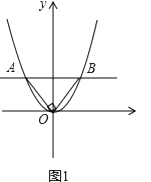
（2）如图2所示，在（1）所求得的抛物线上，当直线AB与x轴不平行，∠AOB仍为90°时，求证：A、B两点横坐标的乘积是一个定值；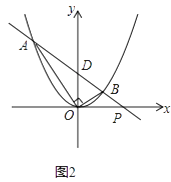
（3）在（2）的条件下，如果直线AB与x轴、y轴分别交于点P、D，且点B的横坐标为
．那么在x轴上是否存在一点Q，使△QDP为等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，点A表示3街与5大道的十字路口，点B表示5街与3大道的十字路口，如果用(3，5)→(4，5)→(5，5)→(5，4)→(5，3)表示由A到B的一条路径，那么你能用同样的方法写出由A到B的其他几条路径吗？请至少给出3种不同的路径．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=k1x+b(k1≠0)与反比例函数
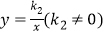的图象交于点A(-1，2)，B(m，-1)．(1)求一次函数与反比例函数的解析式；
(2)在x轴上是否存在点P(n，0)，使△ABP为等腰三角形，请你直接写出P点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市在招商引资期间，把已经破产的油泵厂出租给外地某投资商，该投资商为了减少固定资产投资，将原来400平方米的正方形场地建成300平方米的长方形场地，并且长、宽的比为5:3，并且把原来的正方形铁栅栏围墙全部利用，围成新场地的长方形围墙，请问这些铁栅栏是否够用？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，直线AC∥BD，连接AB，直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连接PA、PB，构成∠PAC、∠APB、∠PBD三个角（提示：有公共端点的两条重合的射线所组成的角是0°）．
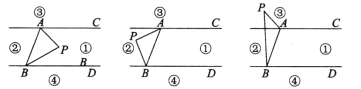
（1）当动点P落在第①部分时，求证：∠APB＝∠PAC＋∠PBD．
（2）当动点P落在第②部分时，∠APB＝∠PAC＋∠PBD是否成立（直接回答成立或不成立）；
（3）当动点P在第③部分时，全面探究∠PAC、∠APB、∠PBD之间的关系，并写出动点P的具体位置和相应的结论．选择其中一种结论加以证明．
相关试题
