【题目】如图,二次函数![]() 的图象与
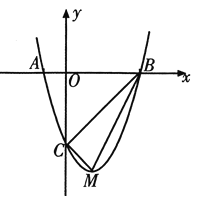
的图象与![]() 轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)△BCM是Rt△;(3)O(0,0),P1(0,
;(2)△BCM是Rt△;(3)O(0,0),P1(0, ![]() ),P2(9,0).
),P2(9,0).
【解析】试题分析:(1)已知抛物线图象上的三点坐标,可用待定系数法求出该抛物线的解析式;
(2)根据B、C、M的坐标,可求得△BCM三边的长,然后判断这三条边的长是否符合勾股定理即可;
(3)假设存在符合条件的P点;首先连接AC,根据A、C的坐标及(2)题所得△BDC三边的比例关系,即可判断出点O符合P点的要求,因此以P、A、C为顶点的三角形也必与△COA相似,那么分别过A、C作线段AC的垂线,这两条垂线与坐标轴的交点也符合点P点要求,可根据相似三角形的性质(或射影定理)求得OP的长,也就得到了点P的坐标.
解:(1)∵二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,
∴![]() ,
,
解得:![]() ,
,
则抛物线解析式为y=x2﹣2x﹣3;
(2)△BCM为直角三角形,理由为:
对于抛物线解析式y=x2﹣2x﹣3=(x﹣1)2﹣4,即顶点M坐标为(1,﹣4),
令x=0,得到y=﹣3,即C(0,﹣3),
根据勾股定理得:BC=3![]() ,BM=2
,BM=2![]() ,CM=
,CM=![]() ,
,
∵BM2=BC2+CM2,
∴△BCM为直角三角形;
(3)若∠APC=90°,即P点和O点重合,如图1,

连接AC,
∵∠AOC=∠MCB=90°,且![]() =
=![]() ,
,
∴Rt△AOC∽Rt△MCB,
∴此时P点坐标为(0,0).
若P点在y轴上,则∠PAC=90°,如图2,过A作AP1⊥AC交y轴正半轴于P1,
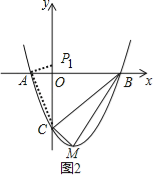
∵Rt△CAP1∽Rt△COA∽Rt△BCM,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴点P1(0,![]() ).
).
若P点在x轴上,则∠PCA=90°,如图3,过C作CP2⊥AC交x轴正半轴于P2,
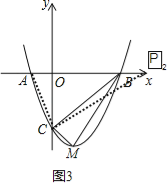
∵Rt△P2CA∽Rt△COA∽Rt△BCM,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,AP2=10,
,AP2=10,
∴点P2(9,0).
∴符合条件的点有三个:O(0,0),P1(0,![]() ),P2(9,0).
),P2(9,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=8,ab=15,则a2+ab+b2=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2﹣3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
(1)图中a值为 .
(2)将跳绳次数在160~190的选手依次记为A1、A2、…An,从中随机抽取两名选手作经验交流,请用树状或列表法求恰好抽取到的选手A1和A2的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线
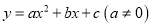 的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(0,3)和(0,4)之间.则下列结论:①
的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(0,3)和(0,4)之间.则下列结论:①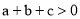 ;②
;②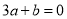 ;③
;③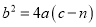 ;④一元二次方程
;④一元二次方程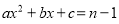 有两个不相等的实数根.其中正确结论的个数是
有两个不相等的实数根.其中正确结论的个数是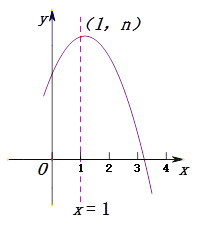
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一个圆柱形的饼干盒,在盒子外侧下底面的点A处有甲、乙两只蚂蚁,它们都想要吃到上底面外侧B′处的食物:甲蚂蚁沿A→A′→B′的折线爬行,乙蚂蚁沿圆柱的侧面爬行:若∠AOB=∠A′O′B′=90°(AA′、BB′都与圆柱的中轴线OO′平行),圆柱的底面半径是12cm,高为1cm,则:
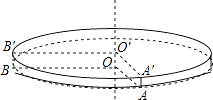
(1)A′B′=cm,甲蚂蚁要吃到食物需爬行的路程长l1=cm;
(2)乙蚂蚁要吃到食物需爬行的最短路程长l2=cm(π取3);
(3)若两只蚂蚁同时出发,且爬行速度相同,在乙蚂蚁采取最佳策略的前提下,哪只蚂蚁先到达食物处?请你通过计算或合理的估算说明理由.(参考数据:π取3,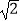 ≈1.4)
≈1.4) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(+26)+(﹣14)+(﹣16)+(+8)
(2)(﹣5.3)+(﹣3.2)﹣(﹣2.5)﹣(+4.8)
(3)(﹣8)×(﹣25)×(﹣0.02)
(4)( ﹣
﹣  +
+  ﹣
﹣ 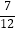 )×(﹣36)
)×(﹣36)
(5)(﹣1)÷(﹣10 )÷(﹣1
)÷(﹣1  )
)
(6)8+(﹣3)2×(﹣2)
(7)0﹣23÷(﹣4)3﹣
(8)100÷(﹣2)2﹣(﹣2)÷(﹣ ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】下面的两个三角形一定全等的是( )
A. 腰相等的两个等腰三角形
B. 一个角对应相等的两个等腰三角形
C. 斜边对应相等的两个直角三角形
D. 底边相等的两个等腰直角三角形
相关试题

