【题目】计算题
(1)(+26)+(﹣14)+(﹣16)+(+8)
(2)(﹣5.3)+(﹣3.2)﹣(﹣2.5)﹣(+4.8)
(3)(﹣8)×(﹣25)×(﹣0.02)
(4)( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() )×(﹣36)
)×(﹣36)
(5)(﹣1)÷(﹣10 ![]() )÷(﹣1
)÷(﹣1 ![]() )
)
(6)8+(﹣3)2×(﹣2)
(7)0﹣23÷(﹣4)3﹣ ![]()
(8)100÷(﹣2)2﹣(﹣2)÷(﹣ ![]() ).
).
参考答案:
【答案】
(1)解:(+26)+(﹣14)+(﹣16)+(+8)=26﹣14﹣16+8=4
(2)解:(﹣5.3)+(﹣3.2)﹣(﹣2.5)﹣(+4.8)=﹣5.3﹣3.2+2.5﹣4.8=﹣10.8
(3)解:(﹣8)×(﹣25)×(﹣0.02)=﹣8×25×0.02=﹣4
(4)解:( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() )×(﹣36)=﹣
)×(﹣36)=﹣ ![]() ×36+
×36+ ![]() ×36﹣
×36﹣ ![]() ×36+
×36+ ![]() ×36=﹣18+20﹣30+21=﹣7
×36=﹣18+20﹣30+21=﹣7
(5)解:(﹣1)÷(﹣10 ![]() )÷(﹣1
)÷(﹣1 ![]() )=﹣1×
)=﹣1× ![]() ×
× ![]() =﹣
=﹣ ![]()
(6)解:8+(﹣3)2×(﹣2)=8﹣9×2=﹣10
(7)解:0﹣23÷(﹣4)3﹣ ![]() =8÷64﹣
=8÷64﹣ ![]() =
= ![]() ﹣
﹣ ![]() =0
=0
(8)解:100÷(﹣2)2﹣(﹣2)÷(﹣ ![]() )=100÷4﹣2×
)=100÷4﹣2× ![]() =25﹣3=22
=25﹣3=22
【解析】(1)消去括号后,再通过有理数的加、减运算即可得出结论;(2)消去括号后,再通过有理数的加、减运算即可得出结论;(3)消去括号后,再通过有理数的乘法运算即可得出结论;(4)利用乘法的分配律将原算式分成四项,先算乘法,再算加、减即可得出结论;(5)将带分数转化成假分数并化除为乘,计算后即可得出结论;(6)算出(﹣3)2并消去括号,再根据有理数的运算顺序,算出结果即可;(7)先算出有理数的乘法,再根据有理数的运算顺序,算出结果即可;(8)先算出有理数的乘法并消去括号,再根据有理数的运算顺序,算出结果即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线
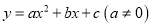 的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(0,3)和(0,4)之间.则下列结论:①
的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(0,3)和(0,4)之间.则下列结论:①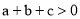 ;②
;②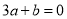 ;③
;③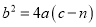 ;④一元二次方程
;④一元二次方程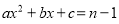 有两个不相等的实数根.其中正确结论的个数是
有两个不相等的实数根.其中正确结论的个数是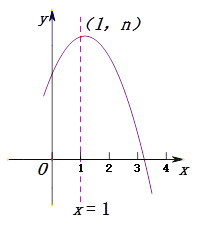
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
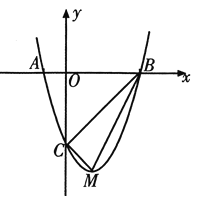
查看答案和解析>>【题目】如图,二次函数
 的图象与
的图象与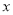 轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一个圆柱形的饼干盒,在盒子外侧下底面的点A处有甲、乙两只蚂蚁,它们都想要吃到上底面外侧B′处的食物:甲蚂蚁沿A→A′→B′的折线爬行,乙蚂蚁沿圆柱的侧面爬行:若∠AOB=∠A′O′B′=90°(AA′、BB′都与圆柱的中轴线OO′平行),圆柱的底面半径是12cm,高为1cm,则:
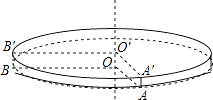
(1)A′B′=cm,甲蚂蚁要吃到食物需爬行的路程长l1=cm;
(2)乙蚂蚁要吃到食物需爬行的最短路程长l2=cm(π取3);
(3)若两只蚂蚁同时出发,且爬行速度相同,在乙蚂蚁采取最佳策略的前提下,哪只蚂蚁先到达食物处?请你通过计算或合理的估算说明理由.(参考数据:π取3,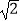 ≈1.4)
≈1.4) -
科目: 来源: 题型:
查看答案和解析>>【题目】下面的两个三角形一定全等的是( )
A. 腰相等的两个等腰三角形
B. 一个角对应相等的两个等腰三角形
C. 斜边对应相等的两个直角三角形
D. 底边相等的两个等腰直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知常数a,b满足x2+ax-10=(x+5)(x+b),则ab=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点E是AD上的一点,∠DBC=∠BED.
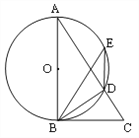
(1)求证:BC是⊙O的切线;
(2)已知AD=3,CD=2,求BC的长.
相关试题

