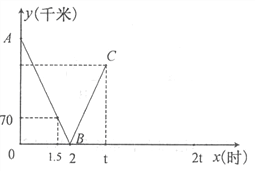
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图中信息:
(1)求线段AB所在直线的函数解析式;
(2) 可求得甲乙两地之间的距离为 千米;
(3)已知两车相遇时快车走了180千米,则快车从甲地到达乙地所需时间为 小时.
参考答案:
【答案】(1)y=-140x+280;(2)280;(3) ![]()
【解析】试题分析:(1)设出AB所在直线的函数解析式,由待定系数法求解即可.
![]() 由解析式可以算出甲乙两地之间的距离.
由解析式可以算出甲乙两地之间的距离.
![]() 两车相遇时快车走了180千米,用了2个小时,可以求出快车的速度,即可求出快车从甲地到达乙地所需时间.
两车相遇时快车走了180千米,用了2个小时,可以求出快车的速度,即可求出快车从甲地到达乙地所需时间.
试题解析:(1)设直线AB的解析式为y=kx+b.
∵直线AB经过点(1.5,70),(2,0),
∴![]()
解得![]()
∴直线AB的解析式为![]()
![]() ∵当x=0时,y=280.
∵当x=0时,y=280.
∴甲乙两地之间的距离为280千米.
故答案为:280.
![]() 两车相遇时快车走了180千米,用了2个小时,快车的速度为:
两车相遇时快车走了180千米,用了2个小时,快车的速度为: ![]() 千米/小时,
千米/小时,
快车从甲地到达乙地所需时间为: ![]() 小时.
小时.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将-2,-1,0,1,2,3,4,5,6,7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的4个数相加,共得5个数,设为a1,a2,a3,a4,a5.
(1)求
 (a1+a2+a3+a4+a5)的值;
(a1+a2+a3+a4+a5)的值;(2)交换其中任何两位数的位置后,
 (a1+a2+a3+a4+a5)的值是否改变?并说明理由.
(a1+a2+a3+a4+a5)的值是否改变?并说明理由.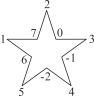
-
科目: 来源: 题型:
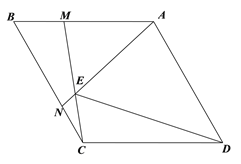
查看答案和解析>>【题目】如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.
(1)证明△BCM≌△CAN;
(2)∠AEM= °;
(3)求证DE平分∠AEC;
(4)试猜想AE,CE,DE之间的数量关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+2的图象与反比例函数y=
 (k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(1)求反比例函数y= (k≠0)的表达式;
(k≠0)的表达式;
(2)若P是y轴上一点,且满足△ABP的面积为6,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.

-
科目: 来源: 题型:
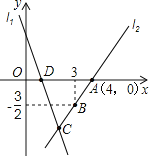
查看答案和解析>>【题目】如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.根据图中信息:
(1)求直线l2的解析表达式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,求出点P的坐标;
(4)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,∠ACB=90°,AC=BC=4,D为BC的中点,
中,∠ACB=90°,AC=BC=4,D为BC的中点, 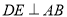 ,垂足为E.过点B作BF//AC交DE的延长线于点F,连接CF,AF.现有如下结论:
,垂足为E.过点B作BF//AC交DE的延长线于点F,连接CF,AF.现有如下结论:①BF=2;②
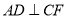 ;③AD平分∠CAB;④AF=
;③AD平分∠CAB;④AF=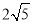 ;⑤∠CAF=∠CFB.其中正确的结论是( )
;⑤∠CAF=∠CFB.其中正确的结论是( )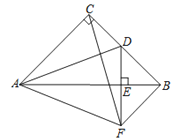
A. ①②③ B. ①②④ C. ②③④⑤ D. ①②④⑤
相关试题

