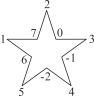
【题目】如图,将-2,-1,0,1,2,3,4,5,6,7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的4个数相加,共得5个数,设为a1,a2,a3,a4,a5.
(1)求![]() (a1+a2+a3+a4+a5)的值;
(a1+a2+a3+a4+a5)的值;
(2)交换其中任何两位数的位置后,![]() (a1+a2+a3+a4+a5)的值是否改变?并说明理由.
(a1+a2+a3+a4+a5)的值是否改变?并说明理由.
参考答案:
【答案】(1)25(2)等于
【解析】
(1)分别算出每一行上的四个数的和,即可得到结果.
(2)由①得,无论位置如何变换,这10个数都要用两遍,那么和不会变化.
解:(1)a1+a2+a3+a4+a5.
=2×(-1-2+0+1+2+3+4+5+6+7).
=50.
(2)交换其中任何两数的位置后,a1+a2+a3+a4+a5的值不变,仍为50.
理由:无论怎样改变位置,其中的每个数都用了两次,即a1+a2+a3+a4+a5.
=2×(-1-2+0+1+2+3+4+5+6+7).
=2×25.
=50.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )

A. S△BEC=2S△CEF B. EF=CF
C. ∠DCF=
 ∠BCD D. ∠DFE=3∠AEF
∠BCD D. ∠DFE=3∠AEF -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)0.36+(-7.4)+0.3+(-0.6)+0.64;(2)3
 +(-2
+(-2 )+5
)+5 +(-8
+(-8 );
);(3)(-103)+(+1
 )+(-97)+(+100)+(-1
)+(-97)+(+100)+(-1 );
);(4)(-2
 )+(-0.38)+(-
)+(-0.38)+(- )+(+0.38);
)+(+0.38);(5)(-9
 )+15
)+15 +(-3
+(-3 )+(-22.5)+(-15
)+(-22.5)+(-15 );
);(6)[(+
 )+(-3.5)+(-6)]+[(+2.5)+(+6)+(+
)+(-3.5)+(-6)]+[(+2.5)+(+6)+(+ )].
)]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD是边AB上的高,且
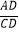 =
=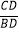 .
.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.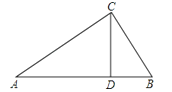
-
科目: 来源: 题型:
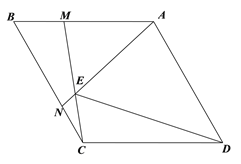
查看答案和解析>>【题目】如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.
(1)证明△BCM≌△CAN;
(2)∠AEM= °;
(3)求证DE平分∠AEC;
(4)试猜想AE,CE,DE之间的数量关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+2的图象与反比例函数y=
 (k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(1)求反比例函数y= (k≠0)的表达式;
(k≠0)的表达式;
(2)若P是y轴上一点,且满足△ABP的面积为6,求点P的坐标.
-
科目: 来源: 题型:
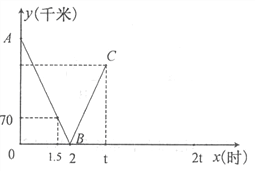
查看答案和解析>>【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图中信息:
(1)求线段AB所在直线的函数解析式;
(2) 可求得甲乙两地之间的距离为 千米;
(3)已知两车相遇时快车走了180千米,则快车从甲地到达乙地所需时间为 小时.
相关试题

