搜索
【题目】如图，一次函数y=x+2的图象与反比例函数y=
（k≠0）的图象交于A，B两点，且点A的坐标为（1，m）．
（1）求反比例函数y=（k≠0）的表达式；
（2）若P是y轴上一点，且满足△ABP的面积为6，求点P的坐标．
参考答案：
【答案】解：（1）∵一次函数图象过A点，
∴m=1+2，解得m=3，
∴A点坐标为（1，3），
又∵反比例函数图象过A点，
∴k=1×3=3，
∴反比例函数y=
（k≠0）的表达式为y=
．
（2）∵
，
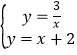解得
或
∴B（﹣3，﹣1），
设直线与y轴的交点为C（0，2），
∵△ABP的面积为6，
∴
PC|xB|+PC|xA|=6，
∴PC（1+3）=6，
∴PC=3，
∴P（0，5）或（0，﹣1）．
【解析】（1）把A点坐标代入一次函数解析式可求得m的值，可得到A点坐标，再把A点坐标代入反比例函数解析式可求得k的值；
（2）联立方程，解方程组即可求得B的坐标，设直线与y轴的交点为C（0，2），根据△ABP的面积为6得出PC|xB|+PC|xA|=6，求出PC的长，即可求得P点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，CD是边AB上的高，且
=
．
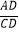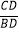（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．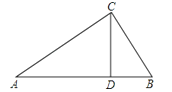
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将－2，－1，0，1，2，3，4，5，6，7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数)，将每一条线上的4个数相加，共得5个数，设为a1，a2，a3，a4，a5.
(1)求
(a1＋a2＋a3＋a4＋a5)的值；(2)交换其中任何两位数的位置后，
(a1＋a2＋a3＋a4＋a5)的值是否改变？并说明理由．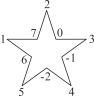
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图菱形ABCD中，∠ADC=60°，M、N分别为线段AB，BC上两点，且BM=CN，且AN，CM所在直线相交于E.
（1）证明△BCM≌△CAN；
（2）∠AEM= °；
（3）求证DE平分∠AEC；
（4）试猜想AE，CE，DE之间的数量关系并证明.
-
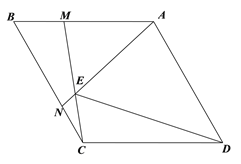
科目： 来源： 题型：
查看答案和解析>>【题目】一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶.设行驶的时间为x(时)，两车之间的距离为y(千米)，图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系．根据图中信息：
（1）求线段AB所在直线的函数解析式；
（2） 可求得甲乙两地之间的距离为 千米；
（3）已知两车相遇时快车走了180千米，则快车从甲地到达乙地所需时间为 小时．
-
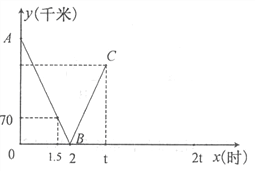
科目： 来源： 题型：
查看答案和解析>>【题目】在平行四边形ABCD中，分别以AD、BC为边向内作等边△ADE和等边△BCF，连接BE、DF．求证：四边形BEDF是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线l1的解析表达式为：y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．根据图中信息：
（1）求直线l2的解析表达式；
（2）求△ADC的面积；
（3）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，求出点P的坐标；
（4）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、D、C、H为顶点的四边形是平行四边形？若存在，请直接写出点H的坐标；若不存在，请说明理由．
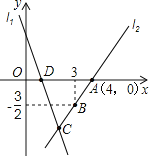
相关试题
