【题目】在平行四边形ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.

参考答案:
【答案】证明见解析.
【解析】试题分析: 由题意先证∠DAE=∠BCF=60°,再由SAS证△DCF≌△BAE,继而题目得证.
试题解析:
∵四边形ABCD是平行四边形,
∴CD=AB,AD=CB,∠DAB=∠BCD.
又∵△ADE和△BCF都是等边三角形,
∴DE=AD=AE,CF=BF=BC,∠DAE=∠BCF=60°.
∴BF=DE,CF=AE,∠DCF=∠BCD-∠BCF,∠BAE=∠DAB-∠DAE,
即∠DCF=∠BAE.
在△DCF和△BAE中,
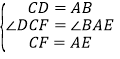
∴△DCF≌△BAE(SAS).
∴DF=BE.
又∵BF=DE,
∴四边形BEDF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
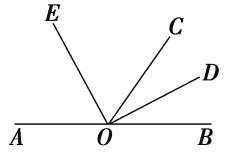
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为( )

A.甲<乙<丙 B.乙<丙<甲
C.丙<乙<甲 D.甲=乙=丙
-
科目: 来源: 题型:
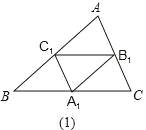
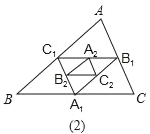
查看答案和解析>>【题目】如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB上的点,且A1C1∥AC,A1B1∥AB,B1C1∥BC,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1上的点,且A2C2∥A1C1,A2B2∥A1B1,B2C2∥B1C1,…,按此规律,则第n个图形中平行四边形的个数共有__个.

-
科目: 来源: 题型:
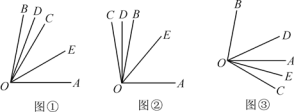
查看答案和解析>>【题目】如图①,已知∠AOB=80°,OC是∠AOB内的一条射线,OD,OE分别平分∠BOC和∠COA.
(1)求∠DOE的度数;
(2)当射线OC绕点O旋转到OB的左侧时如图②(或旋转到OA的右侧时如图③),OD,OE仍是∠BOC和∠COA的平分线,此时∠DOE的大小是否和(1)中的答案相同?若相同,请选取一种情况写出你的求解过程;若不相同,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )
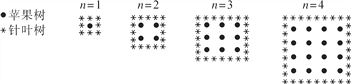
A. 6 B. 8 C. 12 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).

(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
相关试题

