【题目】如图,在![]() 中,∠ACB=90°,AC=BC=4,D为BC的中点,
中,∠ACB=90°,AC=BC=4,D为BC的中点, ![]() ,垂足为E.过点B作BF//AC交DE的延长线于点F,连接CF,AF.现有如下结论:
,垂足为E.过点B作BF//AC交DE的延长线于点F,连接CF,AF.现有如下结论:
①BF=2;②![]() ;③AD平分∠CAB;④AF=
;③AD平分∠CAB;④AF=![]() ;⑤∠CAF=∠CFB.其中正确的结论是( )
;⑤∠CAF=∠CFB.其中正确的结论是( )
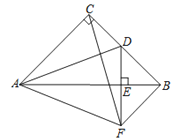
A. ①②③ B. ①②④ C. ②③④⑤ D. ①②④⑤
参考答案:
【答案】D
【解析】(1)∵△ABC中,∠ACB=90°,AC=BC=4,D为BC的中点,
∴BD=CD=2,∠CAB=∠CBA=45°,
∵BF∥AC,DF⊥AB于点E,
∴∠FBA=∠CAB=45°,∠DEB=90°,
∴∠DBF=90°,∠BDF=45°,
∴△DBF是等腰直角三角形,
∴BF=BD=CD=2;即结论①正确;
(2)如下图,∵在△ACD和△CBF中,AC=BC,∠ACD=∠CBF=90°,CD=BF,
∴△ACD≌△CBF,
∴∠CAD=∠BCF,
∵∠ACF+∠BCF=90°,
∴∠ACF+∠CAD=90°,
∴∠AOC=90°,
∴AD⊥CF;即结论②正确;
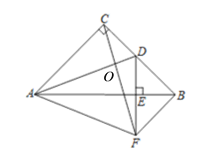
(3)∵△ABC中,∠ACB=90°,AC=BC=4,D为BC的中点,
∴AD是△ABC的中线,但不是△ABC的角平分线;即结论③错误;
(4)由(1)可知,△BDF中,BD=BF,BE⊥DF,
∴AE是DF的垂直平分线,
∴AF=AD,
∵在△ACD中,∠ACD=90°,AC=4,CD=2,
∴AD=![]() ,
,
∴AF=![]() ,即结论④正确;
,即结论④正确;
(5)∵△ACD≌△CBF,
∴AD=CF,
∵AD=AF,
∴AF=CF,
∴∠CAF=∠ACF,
∵BF∥AC,
∴∠ACF=∠CFB,
∴∠CAF=∠CFB;即结论⑤正确.
综上所述,正确的结论是①②④⑤.
故选D.
-
科目: 来源: 题型:
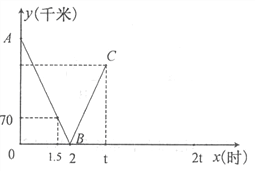
查看答案和解析>>【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图中信息:
(1)求线段AB所在直线的函数解析式;
(2) 可求得甲乙两地之间的距离为 千米;
(3)已知两车相遇时快车走了180千米,则快车从甲地到达乙地所需时间为 小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.

-
科目: 来源: 题型:
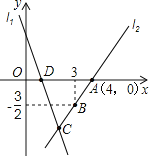
查看答案和解析>>【题目】如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.根据图中信息:
(1)求直线l2的解析表达式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,求出点P的坐标;
(4)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:
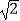 ≈1.41,
≈1.41,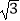 ≈1.73,
≈1.73, ≈2.45)
≈2.45)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AD平分∠CAE,AD∥BC.
(1)求证:△ABC是等腰三角形.
(2)当∠CAE等于多少度时△ABC是等边三角形?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程4(2﹣x)+x=ax的解为正整数,且关于x的不等式组
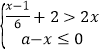 有解,则满足条件的所有整数a的值之和是( )
有解,则满足条件的所有整数a的值之和是( )A. 4 B. 0 C. ﹣1 D. ﹣3
相关试题

