【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨l元,则每个月少卖l0件(每件售价不能高于65元).设每件商品的售价上x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量戈的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?
参考答案:
【答案】
(1)解:由题意得: ![]() ,
,![]()
![]() 且
且 ![]() 为整数
为整数 ![]()
(2)解:由(1)中的 ![]() 与
与 ![]() 的解析式配方得:
的解析式配方得: ![]() .
.
∵ ![]() ,
,
∴当 ![]() 时,
时, ![]() 有最大值2402.5.
有最大值2402.5.
∵ ![]() 且
且 ![]() 为整数,
为整数,
当 ![]() 时,
时, ![]() ,
, ![]() (元);当
(元);当 ![]() 时,
时, ![]() ,
, ![]() (元),
(元),
∴当售价定为每件55或56元时,每个月的利润最大,最大的月利润是2400元 。
(3)解:当 ![]() 时,
时, ![]() ,解得:
,解得: ![]() ,
, ![]() .
.
∴当 ![]() 时,
时, ![]() ;当
;当 ![]() 时,
时, ![]() .
.
∴当售价定为每件51或60元时,每个月的利润为2200元
【解析】(1)设每件商品的售价上x元(x为正整数),每个月的销售利润为y元,则一个月的销量为(21010)件 ,单件的利润为( 50 + x 40 ) 元, 根据销售利润等于销售数量×单件利润,得出y与x的函数关系式;直接写出x的取值范围即可;
(2)将由(1)中的 y 与 x 的解析式配方得: y = 10 ( x 5.5 ) 2 + 2402.5 .由于此函数的二次项系数 a = 10 < 0 ,从而得出当 x = 5.5 时, y 有最大值2402.5.又因0 < x ≤ 15 且 x 为整数,从而得出当 x = 5 时, 50 + x = 55 , y = 2400 (元);当 x = 6 时, 50 + x = 56 , y = 2400 (元);(3)把 y = 2200代入(1)得到的函数解析式,从而得出一个一元二次方程,求解得出x的值,然后得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题成立的有( )
①勾股数是三个正整数 ②全等三角形的三条对应边分别相等
③如果两个实数相等,那么它们的平方相等 ④平行四边形的两组对角分别相等
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
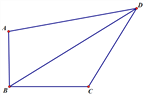
查看答案和解析>>【题目】如图,在四边形ABCD 中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10
 ,
,(1)求四边形ABCD的面积(2)求 BD的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】新农村社区改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2 , 从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元.已知该楼盘每套楼房面积均为120米2 , 若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价l0%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x( ,x取整数)之间的函数关系式;
,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△A'B'C'关于直线MN对称,△A'B'C'和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角∠α的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°则下列结论正确的有( )
(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64°(4)∠BFD=116°.
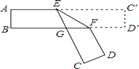
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
相关试题

