搜索
【题目】为了响应“足球进校园”的目标，某校计划为学校足球队购买一批足球，已知购买2个A品牌的足球和3个B品牌的足球共需380元；购买4个A品牌的足球和2个B品牌的足球共需360元．
（1）求A，B两种品牌的足球的单价．
（2）求该校购买20个A品牌的足球和2个B品牌的足球的总费用．
参考答案：
【答案】（1）一个A品牌的足球需90元，则一个B品牌的足球需100元；（2）1900．
【解析】
试题分析：（1）设一个A品牌的足球需x元，则一个B品牌的足球需y元，根据“购买2个A品牌的足球和3个B品牌的足球共需380元；购买4个A品牌的足球和2个B品牌的足球共需360元”列出方程组并解答；
（2）把（1）中的数据代入求值即可．
试题解析：（1）设一个A品牌的足球需x元，则一个B品牌的足球需y元，依题意得：
，解得：
．
答：一个A品牌的足球需90元，则一个B品牌的足球需100元；
（2）依题意得：20×90+2×100=1900（元）．
答：该校购买20个A品牌的足球和2个B品牌的足球的总费用是1900元．
-
科目： 来源： 题型：
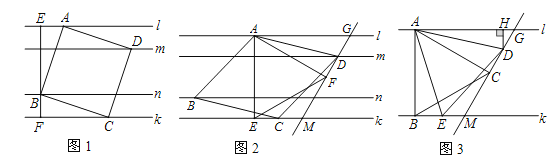
查看答案和解析>>【题目】【背景】已知：l∥m∥n∥k，平行线l与m、m与n、n与k之间的距离分别为d1，d2，d3，且d1＝d3＝1，d2＝2.我们把四个顶点分别在l，m，n，k这四条平行线上的四边形称为“格线四边形” ．
【探究1】(1)如图1，正方形ABCD为“格线四边形”，BE⊥l于点E，BE的反向延长线交直线k于点F.求正方形ABCD的边长．
【探究2】(2)如图2，菱形ABCD为“格线四边形”且∠ADC＝60°，△AEF是等边三角形，AE⊥k于点E，∠AFD＝90°，直线DF分别交直线l，k于点G、点M.求证：EC＝DF．
【拓展】(3)如图3，l∥k，等边△ABC的顶点A，B分别落在直线l，k上，AB⊥k于点B，且∠ACD＝90°，直线CD分别交直线l、k于点G、点M，点D、点E分别是线段GM、BM上的动点，且始终保持AD＝AE，DH⊥l于点H.猜想：DH在什么范围内，BC∥DE？并说明此时BC∥DE的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．
求证：
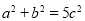．该同学仔细分析后，得到如下解题思路：
先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故
，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证．（1）请你根据以上解题思路帮尤秀同学写出证明过程．
（2）利用题中的结论，解答下列问题：
在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E，F分别为线段AO，DO的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求
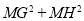的值．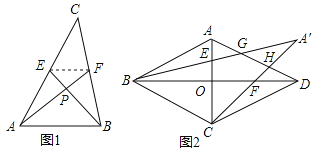
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如果
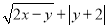=0，求[（x2＋y2）＋2y（x－y）－（x－y）（x+3y）]÷4y的值.（2）先化简，再求值：(2＋a)(2－a)＋a(a－5b)＋3a5b3÷(－a2b)2，其中ab＝－
. -
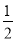科目： 来源： 题型：
查看答案和解析>>【题目】（－2）100比（－2）99大 （ ）
A. 2 B. －2 C. 299 D. 3×299
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各式中，计算正确的是( )
A. 3x＋5y＝8xy B. x6÷x3＝x2 C. x3·x5 ＝x8 D. (－x3)3＝x6
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y＝﹣2x+6的图象与x轴的交点坐标是_____．
相关试题
