【题目】如图1,点![]() 为线段
为线段![]() 上任意一点(不与点
上任意一点(不与点![]() 重合),分别以
重合),分别以![]() 为一腰在
为一腰在![]() 的同侧作等腰
的同侧作等腰![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
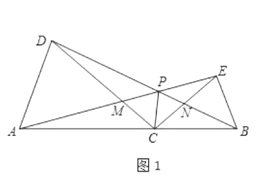
![]() 线段
线段![]() 与
与![]() 的数量关系为 ;请直接写出
的数量关系为 ;请直接写出![]() ;
;
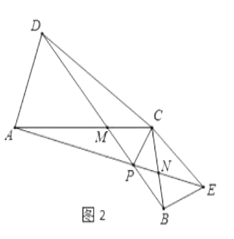
![]() 将
将![]() 绕点
绕点![]() 旋转到如图2所示的位置,其他条件不变,探究线段
旋转到如图2所示的位置,其他条件不变,探究线段![]() 与
与![]() 的数量关系,并说明理由;求出此时
的数量关系,并说明理由;求出此时![]() 的度数;
的度数;
![]() 在
在![]() 的条件下求证:
的条件下求证:![]() .
.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() ,
,![]() ,理由见解析;(3)见解析
,理由见解析;(3)见解析
【解析】
(1)只要证明△ACE≌△DCB,即可解决问题;
(2)只要证明△ACE≌△DCB,即可解决问题;
(3)如图2-1中,分别过C作CH⊥AE,垂足为H,过点C作CG⊥BD,垂足为G,利用面积法证明CG=CH,再利用角平分线的判定定理证明∠DPC=∠EPC即可解决问题;
![]() 如图1中,
如图1中,

∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
∴△ACE≌△DCB.
∴AE=BD,∴CAE=∠CDB,
∵∠AMC=∠DMP,
∴∠APD=∠ACD=30°,
故答案为AE=BD,30°
![]() 如图2中,结论:
如图2中,结论:![]() ,
,![]() .
.
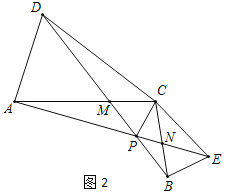
理由:∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
∴△ACE≌△DCB.
∴AE=BD,∴CAE=∠CDB,
∵∠AMP=∠DMC,
∴∠APD=∠ACD=30°.
![]() 证明:如图2-1中,分别过
证明:如图2-1中,分别过![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
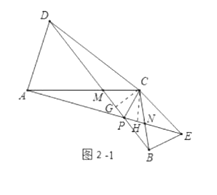
∵△ACE≌△DCB.
∴AE=BD,
∵S△ACE=S△DCB(全等三角形的面积相等),
∴CH=CG,
∴∠DPC=∠EPC(角平分线的性质定理的逆定理),
∵∠APD=∠BPE,
∴∠APC=∠BPC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、
 cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
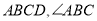 平分线
平分线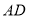 交于点
交于点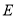 ,连接
,连接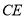 ,过点
,过点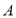 作
作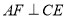 交
交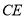 的延长线于点
的延长线于点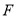 ,连接
,连接 ,则
,则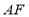 的长为______.
的长为______.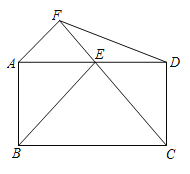
-
科目: 来源: 题型:
查看答案和解析>>【题目】据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒. 问此车是否超过了该路段16米/秒的限制速度?(参考数据:
 ≈1.4,
≈1.4,  ≈1.7)
≈1.7) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
星期
一
二
三
四
五
六
日
增减
+5
-2
-4
+13
-10
+16
-9
(1)根据记录的数据可知该厂星期四生产自行车多少辆;
(2)根据记录的数据可知该厂本周实际生产自行车多少辆;
-
科目: 来源: 题型:
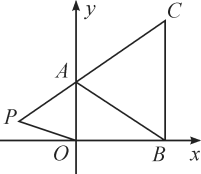
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式
 +(b-3)2=0,(c-4)2≤0.
+(b-3)2=0,(c-4)2≤0.(1)求a,b,c的值;
(2)求出三角形ABC的面积?
(3)如果在第二象限内有一点P(m,
 ),那么请用含m的式子表示四边形ABOP的面积;
),那么请用含m的式子表示四边形ABOP的面积;(4)在(3)的条件下,是否存在点P,使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(
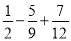 )×(﹣36)
)×(﹣36)(2)计算:100÷(﹣2)2﹣(﹣2)÷(﹣
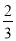 )
)(3)化简:(﹣x2+3xy﹣
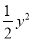 )﹣(﹣
)﹣(﹣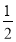 x2+4xy﹣
x2+4xy﹣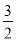 y2)
y2)(4)先化简后求值:x2+(2xy﹣3y2)﹣2(x2+yx﹣2y2),其中x=﹣
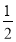 ,y=3.
,y=3.
相关试题

