【题目】使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x-1,令y=0可得x=1,我们就说1是函数y=x-1的零点.
已知y=x2-2mx-2(m+3)(m为常数).
(1)当m=0时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为x1和x2,且![]() ,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式.
,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式.
参考答案:
【答案】(1)![]() 或-
或-![]() (2)y=-
(2)y=-![]() x-1
x-1
【解析】试题分析:(1)根据题中给出的函数的零点的定义,将m=0代入y=x2-2mx-2(m+3),然后令y=0即可解得函数的零点;
(2)令y=0,函数变为一元二次方程,要想证明方程有两个解,只需证明△>0即可;
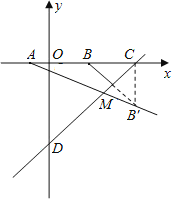
(3)根据题中条件求出函数解析式进而求得A、B两点坐标,个、作点B关于直线y=x-10的对称点B′,连接AB′,求出点B′的坐标即可求得当MA+MB最小时,直线AM的函数解析式.
试题解析:(1)当![]() =0时,该函数为
=0时,该函数为![]() ,令
,令![]() =0,可得
=0,可得![]() ,
,
∴当![]() =0时,求该函数的零点为
=0时,求该函数的零点为![]() 和
和![]() 。
。
(2)令![]() =0,得△=
=0,得△=![]() ,
,
∴无论![]() 取何值,方程
取何值,方程![]() 总有两个不相等的实数根。
总有两个不相等的实数根。
即无论![]() 取何值,该函数总有两个零点
取何值,该函数总有两个零点
(3)依题意有![]() ,
,![]()
由![]() 得
得![]() ,即
,即![]() ,解得
,解得![]() 。
。
∴函数的解析式为![]() 令
令![]() =0,解得
=0,解得![]() 。
。
∵点A在点B左侧,∴A(![]() ),B(4,0)。
),B(4,0)。
作点B关于直线![]() 的对称点B’,连结AB’,则AB’与直线
的对称点B’,连结AB’,则AB’与直线![]() 的交点就是满足条件的M点。易求得直线
的交点就是满足条件的M点。易求得直线![]() 与
与![]() 轴、
轴、![]() 轴的交点分别为C(10,0),D(0,10)。Z.X.X.K]
轴的交点分别为C(10,0),D(0,10)。Z.X.X.K]
连结CB’,则∠BCD=45°,∴BC=CB’=6,∠B’CD=∠BCD=45°。
∴∠BCB’=90°,即B’(![]() )。设直线AB’的解析式为
)。设直线AB’的解析式为![]() ,则Z-X-X-K]
,则Z-X-X-K]
![]() ,解得
,解得![]() ∴直线AB’的解析式为
∴直线AB’的解析式为![]() ,
,
即AM的解析式为![]()
-
科目: 来源: 题型:
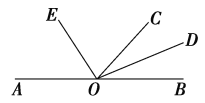
查看答案和解析>>【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
(1)OD与OE的位置关系是______;(2)∠EOC的余角是_______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为9m,则旗杆的高度是多少?(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】读题画图计算并作答
画线段AB=3 cm,在线段AB上取一点K,使AK=BK,在线段AB的延长线上取一点C,使AC=3BC,在线段BA的延长线取一点D,使AD=
 AB.
AB.(1)求线段BC、DC的长?
(2)点K是哪些线段的中点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y =-x+7与正比例函数y=
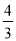 x的图象交于点A,且与x轴交于点B.
x的图象交于点A,且与x轴交于点B.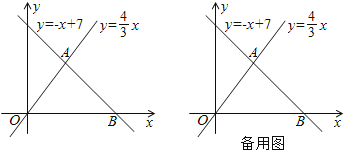
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是直角三角形?若存在,求t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示: (1)按下列语句画出图形:
①延长AC到D,使CD=AC;②反向延长CB到E,使CE=BC;③连接DE.
(2)度量其中的线段和角,你有什么发现?
(3)试判断图中两个三角形的面积是否相等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
等级
A级(优秀)
(≥108分)B级(良好)
(≥84分且<108分)C级(及格)
(≥72分且<84分)D级(不及格)
(<72分)人数
22
28
18
根据以上提供的信息解答下列问题:
(1)若抽取的学生的数学成绩的及格率(C级及其以上为及格)为77.5%,则抽取的学生数是多少人?其中成绩为C级的学生有多少人?
(2)求出D级学生的人数在扇形统计图中的圆心角.
(3)请你估计全县数学成绩为A级的学生总人数.
相关试题

