搜索
【题目】如图，在四边形
中，
，
．
(1)若
于
，
于
，判断
与
数量关系，并说明理由．
(2)如果
，
，求
的度数。
参考答案：
【答案】(1)∠ADB=∠FEC，理由见解析；(2)95°.
【解析】
（1）根据角的关系可以得到AD∥BC，然后得到∠ADB=∠CBD，又BD∥EF，即可得到∠ADB=∠FEC.
（2）由AD∥BC，得到∠C=45°，根据三角形外角性质得到∠DFE的度数.
(1) ∠ADB=∠FEC.
理由如下：
∵
，
∴
，
∴
(同旁内角互补，两直线平行)，
∴
(两直线平行，内错角相等)，
∵
，
∴
∴
(根据垂直于同一直线的两直线平行)，
∴
(两直线平行，同位角相等)，
∴∠ADB=∠FEC.
(2)∵
∴
(两直线平行，同旁内角互补)
∵
∴
∵
∴
(三角形的一个外角等于和它不相邻的两个内角的和)
-
科目： 来源： 题型：
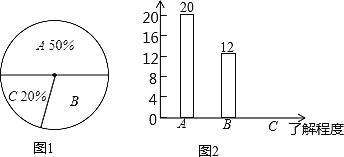
查看答案和解析>>【题目】双峰县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉；B:了解较多；C:一般了解。图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求小刚所在的班级共有多少名学生；
(2)在条形图中,将表示“一般了解”的部分补充完整‘’
(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数；
(4)如果小刚所在年级共1000名同学,请你估算全年级对安全知识“了解较多”的学生人数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，BC＝20 cm，P，Q，M，N分别从A，B，C，D出发，沿AD，BC，CB，DA方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停止．已知在相同时间内，若BQ＝x cm(x≠0)，则AP＝2x cm，CM＝3x cm，DN＝x2 cm，
(1)当x为何值时，点P，N重合；
(2)当x为何值是，以P，Q，M，N为顶点的四边形是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中正确的个数是( )
①若
是完全平方式，则k=3②工程建筑中经常采用三角形的结构，这是利用三角形具有稳定性的性质
③在三角形内部到三边距离相等的点是三个内角平分线的交点
④当
时
⑤若点P在∠AOB内部，D，E分别在∠AOB的两条边上，PD=PE,则点P在∠AOB的平分线上
A.1个B.2个C.3个D.4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP=20°，∠ACP=50°，则∠A+∠P=（ ）
A.70°B.80°C.90°D.100°
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，二次函数y=ax2+bx+c与x轴的交点为（x1，0），（x2，0），且x1＜x2，若方程ax2+bx+c﹣a=0的两根为m，n（m＜n），则下列说法正确的是（ ）
A. x1+x2＞m+n B. m＜n＜x1＜x2 C. x1＜m＜n＜x2 D. m＜x1＜x2＜n
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，∠BAC=30°，AB=12，AD平分∠BAC，点PQ分别是AB、AD边上的动点，则BQ+QP的最小值是（ ）
A.4B.5C.6D.7
相关试题
