【题目】如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD的对称图形为△CED.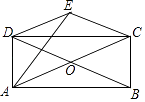
(1)求证:四边形OCED是菱形;
(2)连接AE,若AB=6cm,BC= ![]() cm.
cm.
①求sin∠EAD的值;
②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间.
参考答案:
【答案】
(1)
证明:∵四边形ABCD是矩形.
∴OD=OB=OC=OA,
∵△EDC和△ODC关于CD对称,
∴DE=DO,CE=CO,
∴DE=EC=CO=OD,
∴四边形CODE是菱形.
(2)
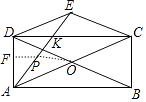
解:①设AE交CD于K.
∵四边形CODE是菱形,
∴DE∥AC,DE=OC=OA,
∴ ![]() =
= ![]() =
= ![]()
∵AB=CD=6,
∴DK=2,CK=4,
在Rt△ADK中,AK= ![]() =
= ![]() =3,
=3,
∴sin∠DAE= ![]() =
= ![]() ,
,
②作PF⊥AD于F.易知PF=APsin∠DAE= ![]() AP,
AP,
∵点Q的运动时间t= ![]() +
+ ![]() =OP+
=OP+ ![]() AP=OP+PF,
AP=OP+PF,
∴当O、P、F共线时,OP+PF的值最小,此时OF是△ACD的中位线,
∴OF= ![]() CD=3.AF=
CD=3.AF= ![]() AD=
AD= ![]() ,PF=
,PF= ![]() DK=1,
DK=1,
∴AP= ![]() =
= ![]() ,
,
∴当点Q沿上述路线运动到点A所需要的时间最短时,AP的长为 ![]() ,点Q走完全程所需的时间为3s.
,点Q走完全程所需的时间为3s.
【解析】(1)只要证明四边相等即可证明;(2)①设AE交CD于K.由DE∥AC,DE=OC=OA,推出 ![]() =
= ![]() =
= ![]() ,由AB=CD=6,可得DK=2,CK=4,在Rt△ADK中,AK=
,由AB=CD=6,可得DK=2,CK=4,在Rt△ADK中,AK= ![]() =
= ![]() =3,根据sin∠DAE=
=3,根据sin∠DAE= ![]() 计算即可解决问题;②作PF⊥AD于F.易知PF=APsin∠DAE=
计算即可解决问题;②作PF⊥AD于F.易知PF=APsin∠DAE= ![]() AP,因为点Q的运动时间t=
AP,因为点Q的运动时间t= ![]() +
+ ![]() =OP+
=OP+ ![]() AP=OP+PF,所以当O、P、F共线时,OP+PF的值最小,此时OF是△ACD的中位线,由此即可解决问题.
AP=OP+PF,所以当O、P、F共线时,OP+PF的值最小,此时OF是△ACD的中位线,由此即可解决问题.
【考点精析】本题主要考查了勾股定理的概念和矩形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(﹣3,2)重合,则点A的坐标是( )
A.(2,5)
B.(﹣8,5)
C.(﹣8,﹣1)
D.(2,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A与∠B互余,∠B与∠C互补,若∠A=50°,则∠C的度数是( )
A.40° B.50° C.130° D.140°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中不能用平方差公式计算的是( )
A. (x-y)(-x+y)B. (-x+y)(-x-y)C. (-x-y)(x-y)D. (x+y)(-x+y)
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:在平面直角坐标系
 中,一张矩形纸片
中,一张矩形纸片 按图
按图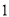 所示放置.已知
所示放置.已知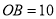 ,
, 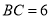 ,将这张纸片折叠,使点
,将这张纸片折叠,使点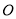 落在边
落在边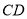 上,记作点
上,记作点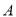 ,折痕与边
,折痕与边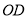 (含端点).
(含端点).交于点
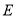 ,与边
,与边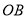 (含端点)或其延长线交于点
(含端点)或其延长线交于点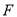 .
.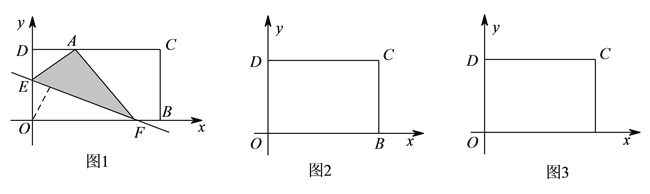
问题探究:
(
 )如图
)如图 ,若点
,若点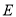 的坐标为
的坐标为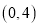 ,直接写出点
,直接写出点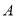 的坐标________;
的坐标________;(
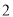 )将矩形沿直线
)将矩形沿直线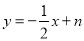 折叠,求点
折叠,求点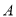 的坐标;
的坐标;问题解决:
(
 )将矩形沿直线
)将矩形沿直线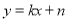 折叠,点
折叠,点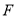 在边
在边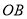 上(含端点),求
上(含端点),求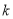 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】二元一次方程x+3y=10的非负整数解共有( )对.
A. 1
B. 2
C. 3
D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据3,5,5,4,5,6的众数是 .
相关试题

