【题目】如图,ABCD中,AB=13,AD=10,将ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( ) 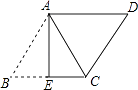
A.5
B.12
C.3
D.![]()
参考答案:
【答案】B
【解析】解:∵翻折后点B恰好与点C重合,
∴AE⊥BC,BE=CE,
∵BC=AD=10,
∴BE=5,
∴AE= ![]() =12,
=12,
∵AD∥BC,
∴点C到AD的距离=AE,
故点C到AD的距离是12,
故选B.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分),还要掌握翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A,点C分别在x轴,y轴上,点B坐标为(4,6),点P从点O出发,以每秒2个单位长度的速度沿O→C→B方向运动,到点B停止.设点P运动的时间为t(秒).
(1)点A的坐标为 ;
(2)当t=1秒时,点P的坐标 ;
(3)当点P在OC上运动,请直接写出点P的坐标(用含有t的式子表示);
(4)在移动过程中,当点P到y轴的距离为1个单位长度时,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)﹣20﹣(﹣18)+(+5)+(﹣9);
(2)(﹣5)×6+(﹣125)÷(﹣5);
(3)(1
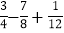 )÷(﹣
)÷(﹣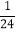 );
);(4)﹣14﹣(1﹣0.5)×
 ×[2﹣(﹣3)2].
×[2﹣(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
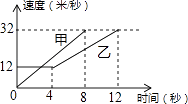
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
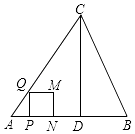
(1)直接写出tanB的值为 .
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为1:3两部分时,直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣x2+bx+c(其中b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
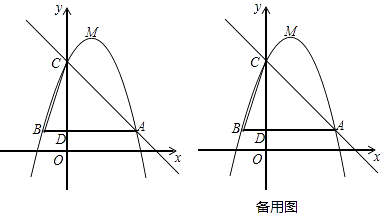
(1)求该二次函数的解析式及点M的坐标.
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
(3)沿直线AC方向平移该二次函数图象,使得CM与平移前的CB相等,求平移后点M的坐标.
(4)点P是直线AC上的动点,过点P作直线AC的垂线PQ,记点M关于直线PQ的对称点为M′.当以点P,A,M,M′为顶点的四边形为平行四边形时,直接写出点P的坐标.
相关试题

