【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB= ![]() ,BC=
,BC= ![]() .
.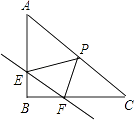
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.
参考答案:
【答案】
(1)
解:如图1,
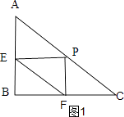
∵E是AB的中点,P是AC的中点,
∴EP∥BC,且EP= ![]() BC,
BC,
∵F是BC的中点,
∴EP∥BF,且EP=BF,
四边形EPFB是平行四边形,
∵∠B=90°,
∴四边形EPFB是矩形
(2)
解:∵AB= ![]() ,BC=
,BC= ![]() .
.
∴BE= ![]() ,BF=
,BF= ![]() ,
,
∴EF= ![]() =1.(2)∵EF∥AC,
=1.(2)∵EF∥AC,
∴∠APE=∠PEF,∵∠EPF=∠A,
∴△APE∽△PEF.
∴ ![]() ,
,
∵AP=1,EF=x,
∴EP2=x,
∴EP= ![]()
(3)
解:如图2,作FH⊥AC交AC于点H,
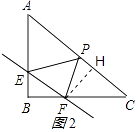
∵EF∥AC,
∴△BEF∽△BAC,
设EF=x,则BF= ![]() x,CF=
x,CF= ![]() ﹣
﹣ ![]() x,
x,
∴FH= ![]() CF=
CF= ![]() ﹣
﹣ ![]() x,
x,
∴S= ![]() EFFH=﹣
EFFH=﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
∴当x=1,即EF=1时,S有最大值为 ![]() .
.
【解析】(1)先求出四边形EPFB是平行四边形,再由∠B=90°得出四边形EPFB是矩形,利用勾股定理求出EF.(2)证明△APE∽△PEF,得出对应边成比例,即可得出结果.(3)作FH⊥AC交AC于点H,设EF=x,得出BF,CF及FH的值,再利用三角形面积求出EF及最大值,利用中位线定理即可求出EP的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,B点的坐标为(4,3).双曲线y=
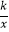 (x>0)过BC的中点P,交AB于点Q.
(x>0)过BC的中点P,交AB于点Q. 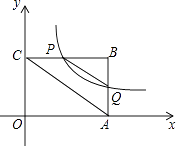
(1)求双曲线的函数表达式及点Q的坐标;
(2)判断线段AC与线段PQ之间的关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D,E分别在AB,AC上,要使DE∥BC,必须具备哪些条件?尽可能把所有条件写出来。

比如:
(1)如果∠DEC+∠ECB=180°,那么DE∥BC:
(2)_________________________________;
(3)_________________________________;
(4)_________________________________;
(5)__________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=
 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.(1)求反比例函数和一次函数的解析式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·
 )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣x+4与x轴、y轴分别交于点A、B,抛物线y=﹣
 (x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
(x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.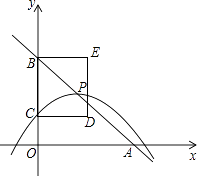
(1)n=(用含m的代数式表示),点C的纵坐标是(用含m的代数式表示);
(2)当点P在矩形BCDE的边DE上,且在第一象限时,求抛物线对应的函数解析式;
(3)直接写出矩形BCDE有两个顶点落在抛物线上时m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小红同学四次中考数学模拟考试成绩分别是:96,104,104,116,关于这组数据下列说法错误的是( )
A.平均数是105
B.众数是104
C.中位数是104
D.方差是50
相关试题

