搜索
【题目】如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为(0，3)，点A在x轴的负半轴上，点D、M分别在边AB、OA上，且AD＝2DB，AM＝2MO，一次函数y＝kx＋b的图象过点D和M，反比例函数y＝
的图象经过点D，与BC的交点为N.
(1)求反比例函数和一次函数的解析式；
(2)若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．
参考答案：
【答案】(1) y＝－
；y＝－x－1(2)(－10，9)或(8，－9)．
【解析】试题分析:本题主要考查一次函数的解析式,反比例函数的解析式以及一次函数图象与性质,(1)首先根据正方形性质得到A,B的坐标,再根据AD=2DB和AM=2MO求出D和M的坐标,最后代入一次函数和反比例函数中求解出解析式,(2)首先求解出N点坐标,之后求出梯形OMNC的面积,再列出△OPM的面积表达式,最后根据
求解出P点的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知BC∥OA，∠B＝∠A＝100°，试回答下列问题：
(1)如图①所示，试说明OB∥AC；
(2)如图②，若点E，F在BC上，且满足∠FOC＝∠AOC，并且OE平分∠BOF.则∠EOC的度数等于________(在横线上填上答案即可)；
(3)在(2)的条件下，若平行移动AC，如图③，那么∠OCB∶∠OFB的值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值；
(4)在(3)的条件下，在平行移动AC的过程中，若使∠OEB＝∠OCA，此时∠OCA的度数等于________(在横线上填上答案即可).
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，过点M(－3，2)分别作x轴、y轴的垂线与反比例函数y＝
的图象交于A，B两点，则四边形MAOB的面积为____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y＝k1x＋b与双曲线y＝
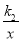相交于点A(1，2)，B(m，－1)两点．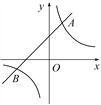
(1)分别求直线和双曲线的表达式；
(2)若A1(x1，y1)，A2(x2，y2)，A3(x3，y3)为双曲线上的三点，且x1<x2<0<x3，请直接写出y1，y2，y3的大小关系．
-
科目： 来源： 题型：
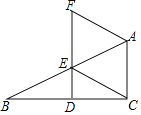
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DF，连接CE、AF．
（1）证明：AF=CE；
（2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标为（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（ ）
A. （
，0） B. （2，0） C. （
，0） D. （3，0）
相关试题
