【题目】小红同学四次中考数学模拟考试成绩分别是:96,104,104,116,关于这组数据下列说法错误的是( )
A.平均数是105
B.众数是104
C.中位数是104
D.方差是50
参考答案:
【答案】D
【解析】解:(A)平均数为: ![]() =105,故A正确; (B)出现最多的数据是104,故B正确;
=105,故A正确; (B)出现最多的数据是104,故B正确;
(C)先排序:96、104、104、116,所以中位数为 ![]() =104,故C正确;
=104,故C正确;
(D)方差为: ![]() [(96﹣105)2+(104﹣105)2+(104﹣105)2+(116﹣105)2]=51,故D错误
[(96﹣105)2+(104﹣105)2+(104﹣105)2+(116﹣105)2]=51,故D错误
故选(D)
【考点精析】解答此题的关键在于理解算术平均数的相关知识,掌握总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数,以及对中位数、众数的理解,了解中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=
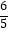 ,BC=
,BC=  .
.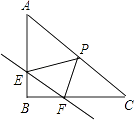
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·
 )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣x+4与x轴、y轴分别交于点A、B,抛物线y=﹣
 (x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
(x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.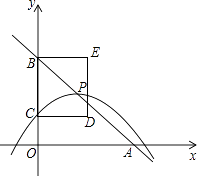
(1)n=(用含m的代数式表示),点C的纵坐标是(用含m的代数式表示);
(2)当点P在矩形BCDE的边DE上,且在第一象限时,求抛物线对应的函数解析式;
(3)直接写出矩形BCDE有两个顶点落在抛物线上时m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )

A.1:3
B.1:5
C.1:6
D.1:11 -
科目: 来源: 题型:
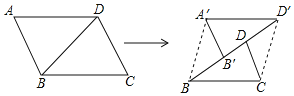
查看答案和解析>>【题目】如图,平行四边形硬纸片ABCD中,
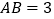 ,
,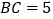 ,
, ,沿着对角线BD将平行四边形剪开成两个三角形,固定
,沿着对角线BD将平行四边形剪开成两个三角形,固定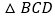 不动,将
不动,将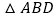 沿射线BD方向以每秒1个单位的速度匀速运动
沿射线BD方向以每秒1个单位的速度匀速运动 运动后
运动后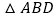 记为
记为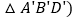 连接
连接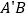 和
和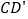 .
.
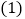 小明认为在运动过程中,始终有
小明认为在运动过程中,始终有 ,你同意吗?请说明理由.
,你同意吗?请说明理由. 保持上述条件不变,当
保持上述条件不变,当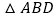 运动______秒时,四边形
运动______秒时,四边形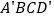 为菱形.
为菱形. 保持上述条件不变,当
保持上述条件不变,当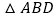 运动______秒时,四边形
运动______秒时,四边形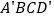 为矩形.
为矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正比例函数
 与反比例函数
与反比例函数 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为 其中
其中 .
. 四边形ABCD的是______
四边形ABCD的是______ 填写四边形ABCD的形状
填写四边形ABCD的形状
 当点A的坐标为
当点A的坐标为 时,四边形ABCD是矩形,求m,n的值.
时,四边形ABCD是矩形,求m,n的值. 试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
相关试题

