搜索
【题目】列方程或不等式组解应用题：
为进一步改善某市旅游景区公共服务设施，市政府预算用资金30万元在二百余家A级景区配备两种轮椅800台，其中普通轮椅每台350元，轻便型轮椅每台450元．
(1) 如果预算资金恰好全部用完，那么能购买两种轮椅各多少台？
(2) 由于获得了不超过5万元的社会捐助，那么轻便型轮椅最多可以买多少台？
参考答案：
【答案】（1）能购买普通轮椅600台，轻便型轮椅200台. （2）最多能购买轻便型轮椅700台．
【解析】
（1）设能购买普通轮椅x台，轻便型轮椅y台.根据两种轮椅800台和预算资金30万元列出方程组求解即可；
（2）设轻便型轮椅可以买a台，根据获得了不超过5万元的社会捐助列不等式求解即可.
解：（1）设能购买普通轮椅x台，轻便型轮椅y台.
根据题意，得
解得
答：能购买普通轮椅600台，轻便型轮椅200台.
（2）设轻便型轮椅可以买a台．
根据题意，得
解得
．
答：最多能购买轻便型轮椅700台．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
2017年年底，共青团北京市委确定了未来3年对口援疆工作内容.在与新疆和田当地教育部门、学校交流过程中，共青团北京市委了解到，和田地区中小学汉语课外读物匮乏.根据对口援疆工作安排，结合和田地区对图书的实际需求，2018年1月5日起，共青团北京市委组织东城、西城、朝阳、海淀、丰台、石景山六个区近900所中小学校，按照和田地区中小学提供的需求图书种类，开展“好书伴成长”募捐书籍活动.活动中，师生踊跃参与，短短两周，已募捐百万余册图书.截至1月19日，分别收到思想理论约2.6万册、哲学约2.6万册、文学艺术约72.6万册、综合约18.0万册，及科学技术五大类书籍，这些图书最终通过火车集中运送至新疆和田.根据相关统计数据，绘制了如下统计图：
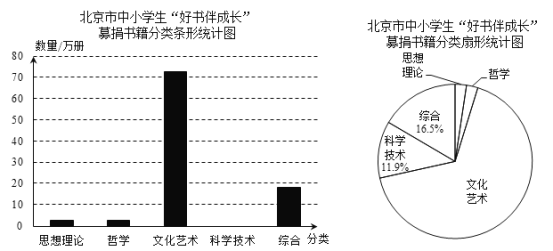
（以上数据来源于新浪网站）
根据以上材料解答下列问题：
（1）此次活动中，北京市中小学生一共捐书约为 万册（保留整数），并将条形统计图补充完整；
（2）在扇形统计图中，文化艺术类所在扇形的圆心角约为 度（保留整数）；
（3）根据本次活动的数据统计分析，写出你对同学们捐书的一条感受或建议．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形ABCD中，E是AB边上一点，且∠A=∠EDF=60°，有下列结论：①AE=BF；②△DEF是等边三角形；③△BEF是等腰三角形；④∠ADE=∠BEF，其中结论正确的个数是（ ）
A. 1 B. 2 C. 3 D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，AB=3，BC=5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于
PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E．
（1）判断四边形ACED的形状，并说明理由；
（2）若BD=8cm，求线段BE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是矩形，把矩形沿对角线AC折叠，点B落在点E处，CE与AD相交于点O．
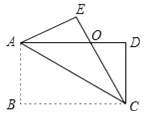
（1）求证：△AOE≌△COD；
（2）若∠OCD=30°，AB=
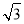，求△AOC的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
已知：如图1，直线AB∥CD，点E是AB、CD之间的一点，连接BE、DE得到∠BED．
求证：∠BED =∠B+∠D.
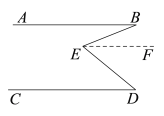图1小冰是这样做的：
证明：过点E作EF∥AB，则有∠BEF=∠B．
∵AB∥CD，∴EF∥CD．
∴∠FED=∠D．
∴∠BEF +∠FED =∠B+∠D．
即∠BED=∠B+∠D．
请利用材料中的结论，完成下面的问题：
已知：直线 AB∥CD，直线MN分别与AB、CD交于点E、F．
（1）如图2，∠BEF和∠EFD的平分线交于点G．猜想∠G的度数，并证明你的猜想；
（2）如图3，EG1和EG2为∠BEF内满足∠1=∠2的两条线，分别与∠EFD的平分线交于点G1和G2．求证：∠FG1 E+∠G2=180°．
相关试题
